题目内容
圆x2+y2=r2(r>0)经过椭圆
+
=1(a>b>0)的两个焦点F1,F2,且与该椭圆有四个不同交点,设P是其中的一个交点,若△PF1F2的面积为26,椭圆的长轴长为15,则a+b+c= (c为半焦距).
| x2 |
| a2 |
| y2 |
| b2 |
分析:依题意作图,易求a=
;利用椭圆的定义与直径三角形△F1PF2即可求得c=
,从而可求得b,继而可得a+b+c的值.
| 15 |
| 2 |
| 11 |
| 2 |
解答: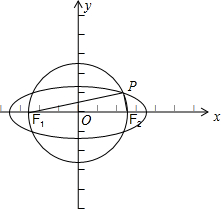 解:依题意知,作图如右:
解:依题意知,作图如右:
∵2a=15,
∴a=
;
又△F1PF2为以F1F2为斜边的直径三角形,且|PF1|+|PF2|=2a=15,
|PF1|•|PF2|=26,|F1F2|=2c,
∴(|PF1|+|PF2|)2=|PF1|2+2|PF1|•|PF2|+|PF2|2=152=225,
即|F1F2|2+2×52=225,
∴4c2=121,
∴c=
,
∴b2=a2-c2=
,
∴b=
,
∴a+b+c=
+
+
=13+
.
故答案为:13+
.
 解:依题意知,作图如右:
解:依题意知,作图如右:∵2a=15,
∴a=
| 15 |
| 2 |
又△F1PF2为以F1F2为斜边的直径三角形,且|PF1|+|PF2|=2a=15,
| 1 |
| 2 |
∴(|PF1|+|PF2|)2=|PF1|2+2|PF1|•|PF2|+|PF2|2=152=225,
即|F1F2|2+2×52=225,
∴4c2=121,
∴c=
| 11 |
| 2 |
∴b2=a2-c2=
| 104 |
| 4 |
∴b=
| 26 |
∴a+b+c=
| 15 |
| 2 |
| 11 |
| 2 |
| 26 |
| 26 |
故答案为:13+
| 26 |
点评:本题考查椭圆的简单性质,着重考查椭圆定义的理解与应用,考查勾股定理的应用,属于中档题.

练习册系列答案
相关题目
已知ab≠0,点M(a,b)是圆x2+y2=r2内一点,直线m是以点M为中点的弦所在的直线,直线l的方程是ax+by=r2,则下列结论正确的是( )
| A、m∥l,且l与圆相交 | B、l⊥m,且l与圆相切 | C、m∥l,且l与圆相离 | D、l⊥m,且l与圆相离 |