题目内容
从圆外一点P(a,b)向圆x2+y2=r2引割线交该圆于A、B两点,求弦AB的中点M的轨迹方程.分析:由题意,令圆心为O,则OM垂直于PM,设M(x,y),表示出两线OM与PM的斜率,因两者垂直,心斜率乘积为-1建立方程即可得出中点M的坐标所满足的方程.
解答: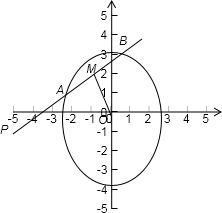 解:设M(x,y),如图,PM⊥OM,因为圆心在原点,故其坐标为(0,0)
解:设M(x,y),如图,PM⊥OM,因为圆心在原点,故其坐标为(0,0)
由公式kPM=
,kOM=
=
故有
×
=-1
整理得(x-
a)2+(y-
b)2=
(a2+b2)(在圆x2+y2=r2内的部分)
答:弦AB的中点M的轨迹方程是(x-
a)2+(y-
b)2=
(a2+b2)(在圆x2+y2=r2内的部分).
 解:设M(x,y),如图,PM⊥OM,因为圆心在原点,故其坐标为(0,0)
解:设M(x,y),如图,PM⊥OM,因为圆心在原点,故其坐标为(0,0)由公式kPM=
| y-b |
| x-a |
| y-0 |
| x-0 |
| y |
| x |
故有
| y-b |
| x-a |
| y |
| x |
整理得(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
答:弦AB的中点M的轨迹方程是(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
点评:考查在坐标系下将几何位置关系转化为方程的能力,通过借助图形找出相关的位置关系来建立方程.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目