题目内容
为综合治理交通拥堵状况,缓解机动车过快增长势头,一些大城市出台了“机动车摇号上牌”的新规.某大城市2012年初机动车的保有量为600万辆,预计此后每年将报废本年度机动车保有量的5%,且报废后机动车的牌照不再使用,同时每年投放10万辆的机动车牌号,只有摇号获得指标的机动车才能上牌.经调研,获得摇号指标的市民通常都会在当年购买机动车上牌.
(1)问:到2016年初,该城市的机动车保有量为多少万辆;
(2)根据该城市交通建设规划要求,预计机动车的保有量少于500万辆时,该城市交通拥堵状况才真正得到缓解.问:至少需要多少年可以实现这一目标.
(参考数据: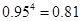 ,
,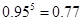 ,
, ,
,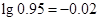 )
)
(1)问:到2016年初,该城市的机动车保有量为多少万辆;
(2)根据该城市交通建设规划要求,预计机动车的保有量少于500万辆时,该城市交通拥堵状况才真正得到缓解.问:至少需要多少年可以实现这一目标.
(参考数据:
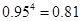 ,
,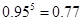 ,
, ,
,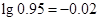 )
)(1)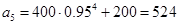 万辆. (2)至少需要8年时间才能实现目标.
万辆. (2)至少需要8年时间才能实现目标.
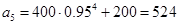 万辆. (2)至少需要8年时间才能实现目标.
万辆. (2)至少需要8年时间才能实现目标.本试题主要是考查了数列在实际生活中的运用,借助于等比数列的概念,和等比数列的通项公式来表示机动车保有量,然后借助于不等式的相关知识,求解对数不等式,得到结论。
(1)首先将实际问题分析,得到关于各年年初机动车保有量的递推关系,然后结合数列的性质,构造得到等比数列,进而得到其通项公式
(2)在第一问的基础上,解关于n的不等式,进而估算法得到结论
(1)设2012年年初机动车保有量为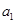 万辆,以后各年年初机动车保有量依次为
万辆,以后各年年初机动车保有量依次为 万辆,
万辆, 万辆,……,每年新增机动车10万辆,则
万辆,……,每年新增机动车10万辆,则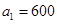 ,
,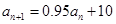 .
.
又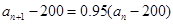 ,且
,且 ,
,
∴ 数列 是以
是以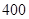 为首项,
为首项,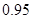 为公比的等比数列.…… …… …… 4分
为公比的等比数列.…… …… …… 4分
∴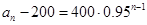 ,即
,即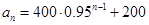 .
.
∴2016年初机动车保有量为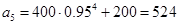 万辆. …… …… 8分
万辆. …… …… 8分
(2)由题可知, ,即
,即 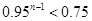 ,
,
∴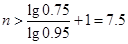 ,故至少需要8年时间才能实现目标
,故至少需要8年时间才能实现目标
(1)首先将实际问题分析,得到关于各年年初机动车保有量的递推关系,然后结合数列的性质,构造得到等比数列,进而得到其通项公式
(2)在第一问的基础上,解关于n的不等式,进而估算法得到结论
(1)设2012年年初机动车保有量为
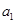 万辆,以后各年年初机动车保有量依次为
万辆,以后各年年初机动车保有量依次为 万辆,
万辆, 万辆,……,每年新增机动车10万辆,则
万辆,……,每年新增机动车10万辆,则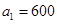 ,
,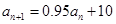 .
. 又
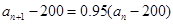 ,且
,且 ,
,∴ 数列
 是以
是以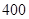 为首项,
为首项,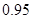 为公比的等比数列.…… …… …… 4分
为公比的等比数列.…… …… …… 4分∴
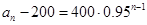 ,即
,即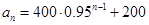 .
.∴2016年初机动车保有量为
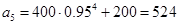 万辆. …… …… 8分
万辆. …… …… 8分(2)由题可知,
 ,即
,即 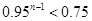 ,
,∴
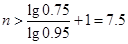 ,故至少需要8年时间才能实现目标
,故至少需要8年时间才能实现目标
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
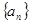 的前n项和为
的前n项和为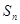 ,且
,且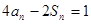 ,数列
,数列 满足
满足 
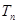 ;
;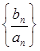 的前项和为
的前项和为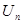 ,求证:
,求证: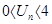 .
.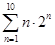 = .
= .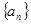 的前
的前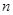 项和为
项和为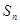 ,且
,且 .
.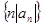 的前
的前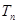 ,求数列
,求数列 的通项公式.
的通项公式.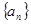 中,
中,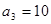 , 则此数列的前5项和为 .
, 则此数列的前5项和为 .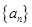 中,
中, ,
,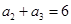 ,则
,则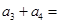
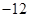
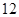
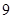
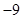
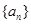 中,
中,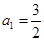 ,
,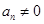 ,且
,且 ,则
,则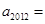 ___
___