题目内容
(本题满分13分) 的三个内角
的三个内角 依次成等差数列.
依次成等差数列.
(Ⅰ)若 ,试判断
,试判断 的形状;
的形状;
(Ⅱ)若 为钝角三角形,且
为钝角三角形,且 ,求
,求
的取值范围.
【答案】
(1)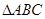 为正三角形;(2)
为正三角形;(2)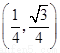 .
.
【解析】本试题主要是考查了解三角形的运用,以及数列的性质的综合运用。
第一问中,利用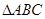 的三个内角
的三个内角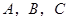 依次成等差数列.得到角B,然后利用
依次成等差数列.得到角B,然后利用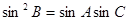 得到
得到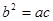 ,结合余弦定理得到a=c,然后判定形状即可
,结合余弦定理得到a=c,然后判定形状即可
第二问中,因为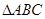 为钝角三角形,且
为钝角三角形,且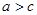 ,那么则可以由=
,那么则可以由= 化简为f(A)=
化简为f(A)=
利用角A的范围求解值域。
解:(Ⅰ)∵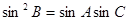 , ∴
, ∴ 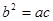 . ∵
. ∵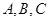 依次成等差数列,
依次成等差数列,
∴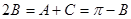 ,
,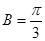 .
由余弦定理
.
由余弦定理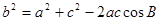 ,
,
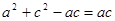 ,∴
,∴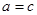 . ∴
. ∴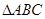 为正三角形……………………6分
为正三角形……………………6分
(Ⅱ)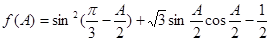 =
=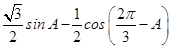
= =
= =
= ……10分
……10分
∵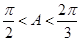 , ∴
, ∴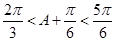 , ………………11分
, ………………11分
∴ 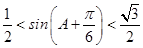 ,
, 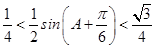
∴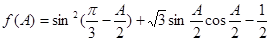 的取值范围是
的取值范围是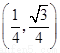 ……13分
……13分

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目

 和
和 ,从集合
,从集合 中随机取一个数作为
中随机取一个数作为 ,从
,从 中随机取一个数作为
中随机取一个数作为 ,求函数
,求函数 在区间
在区间 上是增函数的概率;
上是增函数的概率;  是区域
是区域 内的随机点,求函数
内的随机点,求函数 中,已知
中,已知

 侧面
侧面

 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).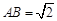 ,求二面角
,求二面角 的大小.
的大小. 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,
, ,求
,求 的值.
的值.