Question

（本题满分13分）

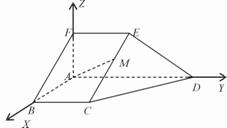
如图，在五面体ABCDEF中，FA平面ABCD，AD//BC//FE，ABAD，AF＝AB＝BC＝FE＝AD.

（Ⅰ）求异面直线BF与DE所成角的余弦值；

（Ⅱ）在线段CE上是否存在点M，使得直线AM与平面CDE所成角的正弦值为？若存在，试确定点M的位置；若不存在，请说明理由.

 

 

 

 

 

 

Answer 1

【答案】

 

 

解法一：建立如图所示的直角坐标系，不妨设AB＝１

则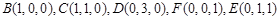                        ………………2分

（Ⅰ）

　　　　　         ………………5分

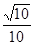　　　　异面直线BF与DE所成角的余弦值为.                 ………………6分

　　（Ⅱ）设平面CDE的一个法向量为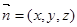

　　

解法二：（Ⅰ）不妨设AB＝１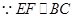，且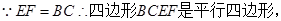

∴∠CED异面直线BF与DE所成角                              ………………3分

CE=BF=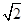,ED=DC=,

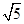所以，异面直线BF与DE所成角的余弦值为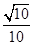                     ………………6分

【解析】略