题目内容
14．已知集合A={x|x=5-4a+a2，a∈R}，B={x|x=4b2+4b+2，b∈R}，判定集合A与B的关系．分析 先对两个二次函数进行配方，求出函数的值域，即得集合A和B，再判定集合A与B的关系．
解答 解：由题意得，a∈R和b∈R，
对于A：x=a2-4a+5=（a-2）2+1≥1，则A=[1，+∞），
对于B：y=4b2+4b+2=4（b2+b）+2=4（b+$\frac{1}{2}$）2+1≥1，则B=[1，+∞），
∴A=B．
点评 本题考查了集合的包含关系判断，解答此题的关键是利用配方法求集合，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
．
；
，若
，求实数
的取值集合．
5．
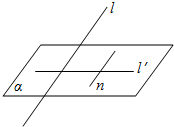如图，设直线l是平面α的一条射线，l′是l在α内的射影，直线n?α．用＜a，b＞表示直线a，b的夹角．求证：
（1）cos＜l，n＞=cos＜l，l′＞•cos＜l′，n＞；
（2）n⊥l?n⊥l′．
如图，设直线l是平面α的一条射线，l′是l在α内的射影，直线n?α．用＜a，b＞表示直线a，b的夹角．求证：（1）cos＜l，n＞=cos＜l，l′＞•cos＜l′，n＞；
（2）n⊥l?n⊥l′．
2．已知函数f（x）=ax3+bx2+cx+d的图象如图所示，则下列判断正确的是（ ）
| A． | a＜0，b＜0，c＜0 | B． | a＞0，b＞0，c＜0 | C． | a＞0，b＜0，c＞0 | D． | a＞0，b＞0，c＞0 |
9．若函数f（x）=|ex+x2-x-m|-2有两个零点，则m的取值范围为（ ）
| A． | （-1，3） | B． | （-3，1） | C． | （3，+∞） | D． | （-∞，1） |
