Question

5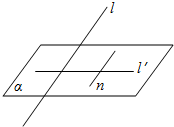．如图，设直线l是平面α的一条射线，l′是l在α内的射影，直线n?α．用＜a，b＞表示直线a，b的夹角．求证：
（1）cos＜l，n＞=cos＜l，l′＞•cos＜l′，n＞；
（2）n⊥l?n⊥l′．

Answer 1

分析 （1）设直线l与平面α交于点A，并在l上取不同于点B的一点B，作BO⊥α，交α于O，作AC，并设n，则AO为l′，在平面α内过O作OC⊥AC，交AC于C点，连结BC，由三垂线定理得AC⊥BC，由此能证明cos＜l，n=cos＜l，l′＞•cos＜l′，n＞．
（2）由已知条件，利用三垂线定理及其逆定理能证明n⊥l?n⊥l′．

解答 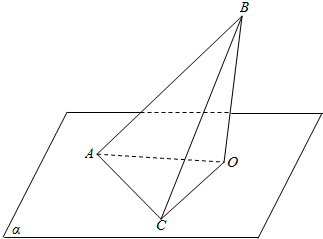证明：（1）如图，AB是平面α的斜线，BO⊥α，交α于O，AC?α，
设AB为l，AC为n，则AO为l′，
在平面α内过O作OC⊥AC，交AC于C点，
连结BC，由三垂线定理得AC⊥BC，
∴cos＜l，n＞=cos∠BAC=$\frac{AC}{AB}$，
cos＜l，l′＞=cos∠BAO=$\frac{AO}{AB}$，
cos＜l′，n＞=cos∠CAO=$\frac{AC}{AO}$，
∴cos＜l，n＞=$\frac{AC}{AB}=\frac{AO}{AB}•\frac{AC}{AO}$=cos＜l，l′＞•cos＜l′，n＞．
（2）n⊥l，即AC⊥AB，
又BO⊥α，AC?α，∴AC⊥BO，
又AB∩BO=B，∴AC⊥平面SAO，
∴AC⊥AO，即n⊥l′；
n⊥l′，即AC⊥AO，
又BO⊥α，AC?α，∴AC⊥BO，
又AO∩BO=O，∴AC⊥平面ABO，
∴AC⊥AB，即n⊥l．
∴n⊥l?n⊥l′．

点评 本题考查异面直线所成角的余弦值的应用，考查直线垂直的证明，是中档题，解题时要认真审题，注意三垂线定理及逆定理的合理运用．