Question

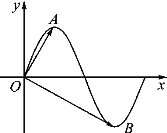
【题目】已知函数，函数的图像在处的切线方程为：

（1）求的值；

（2）若，成立，求的取值范围.

Answer 1

【答案】(1)a=b=1;(2)(2,+∞).

【解析】

（1）对函数求导，在切点的导函数值就是切线的斜率，求出a、b的值；

（2）将原式化简，变为新函数，对新函数求导讨论单调性求出k的取值；

或是利用参变分离求最值，求得k的取值.

解：(1)f(x) =a ∴f(1) =a= ，f(1)= =，

解得a=b=1

∴f(x)= +

(2) (方法1)由+< +得， <0，∵x>0∴lnx+(1k)xk+3<0恒成立

设g(x)=lnx+(1k)xk+3 (x>0)

g(x)= +1k=

当k≤1时，g(x)≥0，y=g(x)在x(0,+∞)上单调递增，不符合题意，舍去

当k>1时，y=g(x)在x(0,)上单调递增，在x(,+∞)上单调递减，

∴g(x)≤g()=ln+2k<0

设h(k)= 2kln(k1),h(k)=1<0,y=h(k)在k(1,+∞)上单调递减

∵h(2)=0∴由h(k)<0解得k>2

综上所述，k的取值范围是(2,+∞).

（方法2）由+< +得， <0，∵x>0∴lnx+(1k)xk+3<0恒成立，

整理得：k> ，

令g(x)=,则g(x)=.

令h(x)= -lnx-3, (x>0),h(x)= - - <0在x>0时恒成立

所以，h(x)单调递减，又h(1)=0，

所以，x∈(0,1)，h(x)>0,即g(x) >0, g(x)单调递增

x∈(1,+∞)，h(x)<0, 即g(x) <0， g(x)单调递减

g(x)在x=1处有最大值g(1)= 2

所以k>2,k的取值范围是(2,+∞)