题目内容
点P在平面ABC上的射影为O,且PA、PB、PC两两垂直,那么O是△ABC的
垂心
垂心
.(填:外心,内心,重心,垂心)分析:根据题意画出图形,如图P是△ABC所在平面外一点,O是P点在平面ABC上的射影.然后利用线面的位置关系进行判定即可.
解答: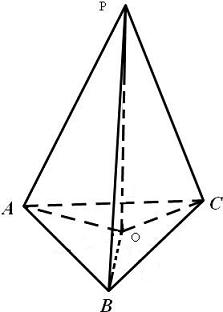 解:若PA、PB、PC两两互相垂直,
解:若PA、PB、PC两两互相垂直,
可得AP⊥平面PBC,BP⊥平面PAC,CP⊥平面PAB,
由此可证得BC⊥OA,AB⊥OC,AC⊥OB,
即此时点O是三角形三边高的交点,
故此时点O是三角形的垂心,
故应填:垂心.
故答案为:垂心.
 解:若PA、PB、PC两两互相垂直,
解:若PA、PB、PC两两互相垂直,可得AP⊥平面PBC,BP⊥平面PAC,CP⊥平面PAB,
由此可证得BC⊥OA,AB⊥OC,AC⊥OB,
即此时点O是三角形三边高的交点,
故此时点O是三角形的垂心,
故应填:垂心.
故答案为:垂心.
点评:本题考查棱锥的结构特征,考查学生发现问题解决问题的能力,是中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
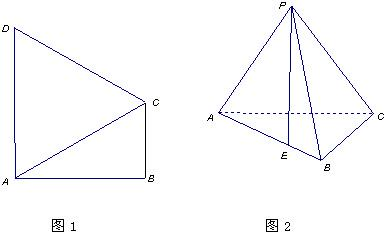 如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=1,AD=CD,把△DAC沿对角线AC折起后如图2所示(点D记为点P),点P在平面ABC上的正投影E落在线段AB上,连接PB.
如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=1,AD=CD,把△DAC沿对角线AC折起后如图2所示(点D记为点P),点P在平面ABC上的正投影E落在线段AB上,连接PB. (2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.
(2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.