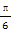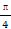题目内容
(本小题满分12分)已知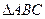 中∠ACB=90°,AS=BC=1,AC=2,SA⊥面ABC,AD⊥SC于D,
中∠ACB=90°,AS=BC=1,AC=2,SA⊥面ABC,AD⊥SC于D,
(1)求证: AD⊥面SBC;
(2)求二面角A-SB-C的大小.
(1) 证明: 

又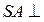 面
面

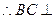 面
面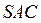 …………2分
…………2分∵ AD
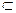 平面SAC,
平面SAC, 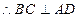 ……………4分
……………4分又
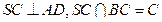

 面
面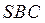 ………6分
………6分(2)由(1)AD⊥面SBC,过D作DE⊥BS交BS于E,连结AE,
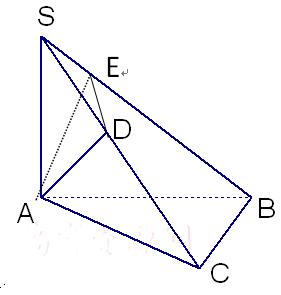
则∠AED为二面角A-SB-C的平面角,………8分,
由AS=BC=1,AC=2,得AD=
 ,………….10分
,………….10分在直角△ADE中,
 ,即二面角A-SB-C的大小为
,即二面角A-SB-C的大小为 ………12分.
………12分.
解析

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
在空间直角坐标系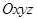 中,已知
中,已知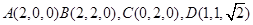 .若
.若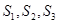 分别是三棱锥
分别是三棱锥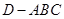 在
在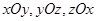 坐标平面上的正投影图形的面积,则( )
坐标平面上的正投影图形的面积,则( )
A.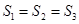 | B.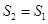 且 且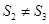 |
C.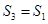 且 且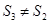 | D.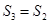 且 且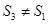 |
若三点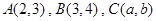 共线,则有( )
共线,则有( )
A.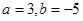 | B.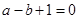 | C.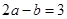 | D.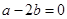 |
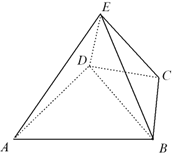
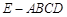 是四棱锥,△
是四棱锥,△ 为正三角形,
为正三角形, .
.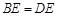 ;
;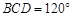 ,M为线段AE的中点,求证:
,M为线段AE的中点,求证: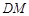 ∥平面
∥平面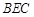 .
.
 中,
中, ,
,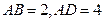 将
将 沿
沿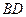 折起到
折起到 的位置,使平面
的位置,使平面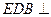 平面
平面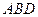
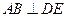 (Ⅱ)求三棱锥
(Ⅱ)求三棱锥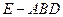 的侧面积。
的侧面积。
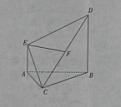
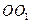 内有一个三棱柱
内有一个三棱柱 ,三棱柱的 底面为圆柱
,三棱柱的 底面为圆柱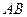 是圆
是圆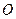 的直径。
的直径。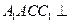 平面
平面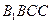 ;
;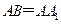 ,在圆
,在圆 柱
柱 。
。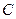 在圆周上运动时,求
在圆周上运动时,求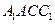 与平面
与平面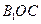 所成的角为
所成的角为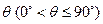 。当
。当
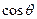 的值。
的值。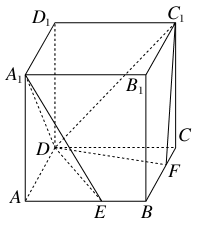
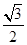 B.
B.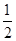 C.
C. D.
D.