题目内容
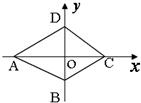如图，已知四边形ABCD在映射f：（x，y）→（x+1，2y）作用下的象集为四边形A1B1C1D1，若四边形A1B1C1D1的面积是12，则四边形ABCD的面积是（ ）| A、9 | ||
| B、6 | ||
C、6
| ||
| D、12 |
分析：由题意可知映射是左右平移和纵坐标的伸缩变换，通过变换，得到面积的关系即可求出选项．
解答：解：因为映射f：（x，y）→（x+1，2y）之间的一一对应是纯一次函数的线性关系，
所以这种作用相当于是将横坐标向左平移1个单位，纵坐标变为为原来的两倍，
所以S′=
S=6
故选B
所以这种作用相当于是将横坐标向左平移1个单位，纵坐标变为为原来的两倍，
所以S′=
| 1 |
| 2 |
故选B
点评：本题是基础题，实质上考查图象的变换，平移与伸缩变换，常用方法：如果映射f：（x，y）→（ay，1-bx），则S′=|a||b|S 这种方法比较抽象．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
如图，已知四边形ABCD为直角梯形，∠ABC=90°，AD∥BC，AD=2，AB=BC=1，沿AC将△ABC折起，使点B到点P的位置，且平面PAC⊥平面ACD．
（几何证明选讲选做题）如图，已知四边形ABCD内接于⊙O，且AB为⊙O的直径，直线MN切
如图：已知四边形ABCD是正方形，PD⊥平面ABCD，PD=AD，点E，F分别是线段PB，AD的中点
如图，已知四边形ABCD为直角梯形，∠ABC=90°，AD∥BC，AD=2，AB=BC=1，沿AC将△ABC折起，使点B到点P的位置，且平面PAC⊥平面ACD．
如图，已知四边形ABCD是菱形，PA⊥平面ABCD，PA=AB=BD=2，AC与BD交于E点，F是PD的中点．