题目内容
 如图:已知四边形ABCD是正方形,PD⊥平面ABCD,PD=AD,点E,F分别是线段PB,AD的中点
如图:已知四边形ABCD是正方形,PD⊥平面ABCD,PD=AD,点E,F分别是线段PB,AD的中点(1)求证:FE∥平面PCD;
(2)求异面直线DE与AB所成的角的余弦值.
分析:(1)取PC的中点G,证明四边形EFGD是平行四边形,可得EF∥GD,证得EF∥平面PDC.
(2)根据CD∥AB,可得∠EDC或其补角为异面直线DE与AB所成的角,△DEC中,利用余弦定理即可得到结论.
(2)根据CD∥AB,可得∠EDC或其补角为异面直线DE与AB所成的角,△DEC中,利用余弦定理即可得到结论.
解答: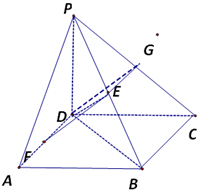 (1)证明:取PC的中点G,连接EG,GD,则EG∥
(1)证明:取PC的中点G,连接EG,GD,则EG∥
BC,且EG=
BC
∴GE∥DF且GE=DF.
∴四边形EFGD是平行四边形.
∴EF∥GD,
又EF?平面PDC,DG?平面PDC,
∴EF∥平面PDC;
(2)解:∵CD∥AB
∴∠EDC或其补角为异面直线DE与AB所成的角
设PD=AD=1,则△DEC中,DE=EC=
,DC=1
∴cos∠EDC=
=
.
 (1)证明:取PC的中点G,连接EG,GD,则EG∥
(1)证明:取PC的中点G,连接EG,GD,则EG∥| 1 |
| 2 |
| 1 |
| 2 |
∴GE∥DF且GE=DF.
∴四边形EFGD是平行四边形.
∴EF∥GD,
又EF?平面PDC,DG?平面PDC,
∴EF∥平面PDC;
(2)解:∵CD∥AB
∴∠EDC或其补角为异面直线DE与AB所成的角
设PD=AD=1,则△DEC中,DE=EC=
| ||
| 2 |
∴cos∠EDC=
| DE2+DC2-EC2 |
| 2DE•DC |
| ||
| 3 |
点评:本题考查证明线面平行,考查线线角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.
如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD. (几何证明选讲选做题)如图,已知四边形ABCD内接于⊙O,且AB为⊙O的直径,直线MN切
(几何证明选讲选做题)如图,已知四边形ABCD内接于⊙O,且AB为⊙O的直径,直线MN切 如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.
如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD. 如图,已知四边形ABCD是菱形,PA⊥平面ABCD,PA=AB=BD=2,AC与BD交于E点,F是PD的中点.
如图,已知四边形ABCD是菱形,PA⊥平面ABCD,PA=AB=BD=2,AC与BD交于E点,F是PD的中点.