Question

（2011•怀化一模）已知实数r，少满足

x-y+6≥0 x+y≥0 x≤3

，z=ax+y的最大值为3a+9，最小值为3a-3，则实数a的取值范围为

[-1，1]

．

Answer 1

分析：作出题中不等式组表示的平面区域，得如图的△ABC及其内部，再根据题意建立关于a的不等式组，解之即可得出实数a的取值范围．

解答：解：作出不等式组

x-y+6≥0 x+y≥0 x≤3

表示的平面区域，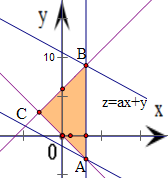
得到如图的△ABC及其内部，其中
A（3，-3），B（3，9），C（-3，3），
设z=F（x，y）=2x-y，把A、B、C坐标分别代入得
F（3，-3）=3a-3，F（3，9）=3a+9，F（-3，3）=-3a+3
 结合题意，可得

3a+9≥-3a+3 -3a+3≥3a-3

，解之得-1≤a≤1．
∴实数a的取值范围为[-1，1]
故答案为：[-1，1]

点评：本题给出二元一次不等式组，在已知目标函数最值的情况下求参数a的范围，着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，属于基础题．