题目内容
11.球坐标(2,$\frac{π}{6}$,$\frac{π}{3}$)对应的直角坐标为:$({\frac{1}{2},\frac{{\sqrt{3}}}{2},\sqrt{3}})$.分析 利用球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系:x=rsinθcosφ,y=rsinθsinφ,z=rcosθ,代入可得M的直角坐标.
解答 解:∵M的球坐标为(2,$\frac{π}{6}$,$\frac{π}{3}$),
∴r=2,θ=$\frac{π}{6}$,φ=$\frac{π}{3}$,
∴x=rsinθcosφ=2•$\frac{1}{2}$•$\frac{1}{2}$=$\frac{1}{2}$,
y=rsinθsinφ=2•$\frac{1}{2}$•$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
z=rcosθ=2•$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
故M的直角坐标为$({\frac{1}{2},\frac{{\sqrt{3}}}{2},\sqrt{3}})$.
故答案为:$({\frac{1}{2},\frac{{\sqrt{3}}}{2},\sqrt{3}})$.
点评 假设P(x,y,z)为空间内一点,则点P也可用这样三个有次序的数r,φ,θ来确定,其中r为原点O与点P间的距离,θ为有向线段OP与z轴正向的夹角,φ为从正z轴来看自x轴按逆时针方向转到OM所转过的角,这里M为点P在xOy面上的投影.这样的三个数r,φ,θ叫做点P的球面坐标,显然,这里r,φ,θ的变化范围为r∈[0,+∞),φ∈[0,2π],θ∈[0,π].

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
12.在△ABC中,已知$\overrightarrow{AB}•\overrightarrow{AC}$=2$\sqrt{3}$,A=60°,则△ABC的面积为( )
| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
1.若(a+b+c)(b+c-a)=3bc且sinA=2sinBcosC,则△ABC是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
 是等差数列,公差
是等差数列,公差 ,
, ,
,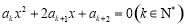 .
. 取不同正整数时,方程都有公共根;
取不同正整数时,方程都有公共根; ,
, ,
,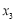 ,…,
,…, ,求证:
,求证: ,
, ,
, ,…,
,…, ,…是等差数列.
,…是等差数列. 中,若
中,若 ,则( )
,则( )

 或
或
 如图,已知圆O:x2+y2=4与轴正半轴交于点P,A(-1,0),B(1,0),直线l与圆O切于点S(l不垂直于x轴),抛物线过两点A,B且以l为准线.
如图,已知圆O:x2+y2=4与轴正半轴交于点P,A(-1,0),B(1,0),直线l与圆O切于点S(l不垂直于x轴),抛物线过两点A,B且以l为准线.