题目内容
(本题满分15分)设函数 .
.
(Ⅰ)若函数 在
在 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数 的最大值;
的最大值;
(Ⅱ)若 对任意的
对任意的 ,
, 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.
注: 为自然对数的底数.
为自然对数的底数.
【答案】
(Ⅰ)b的最大值是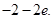 (Ⅱ)
(Ⅱ)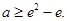
【解析】本题主要考查函数的单调性、导数的运算法则、导数应用、恒成立问题等基础知识,同时考查抽象概括、推理论证能力.
(1) 解: 由题设可知
由题设可知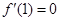 ,
,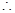
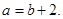
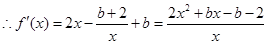
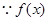 在
在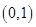 上单调递增,在
上单调递增,在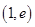 上单调递减,
上单调递减,
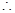
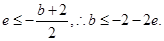
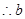 的最大值是
的最大值是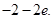
(2)令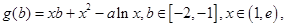
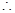
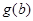 可看作关于
可看作关于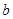 的一次函数且单调递增,
的一次函数且单调递增,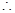 只需
只需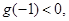 即
即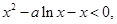
构造函数得到结论。
(Ⅰ)解:
由题设可知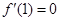 ,
,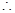
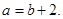

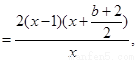
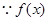 在
在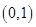 上单调递增,在
上单调递增,在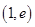 上单调递减,
上单调递减,
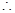
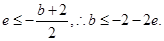
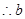 的最大值是
的最大值是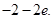
(Ⅱ)解:令
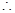
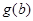 可看作关于
可看作关于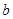 的一次函数且单调递增,
的一次函数且单调递增,
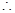 只需
只需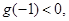 即
即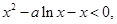
令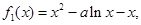 则
则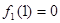 ,
, 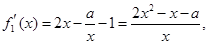
令 ,
,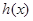 的对称轴为
的对称轴为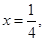
(ⅰ)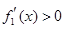 对
对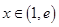 恒成立,
恒成立,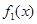 在
在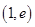 上单调递增,
上单调递增,
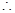
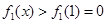 ,不合题意.
,不合题意.
(ⅱ)
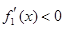 对
对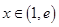 恒成立,
恒成立,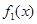 在
在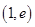 上单调递减,
上单调递减,
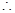
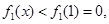 满足题意.
满足题意.
此时只需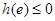 ,
,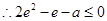 ,
,
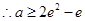 .
.
(ⅲ)在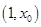 上
上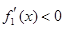 ,在
,在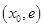 上
上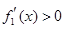 ,
,
即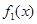 在
在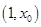 上单调递减,在
上单调递减,在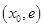 上单调递增.
上单调递增.
此时只需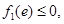
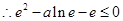 ,
,
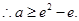
又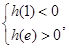 即
即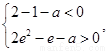

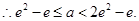
综上,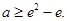
(用分离参数方法解同样给分

练习册系列答案
相关题目
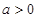 ,函数
,函数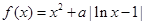 .
. 时,求函数
时,求函数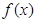 的单调增区间;
的单调增区间; 时,不等式
时,不等式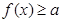 恒成立,实数
恒成立,实数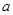 的取值范围.
的取值范围.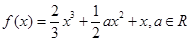 .
.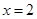 时,
时,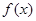 取得极值,求
取得极值,求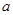 的值;
的值;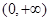 内为增函数,求
内为增函数,求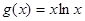 ,是否存在正实数
,是否存在正实数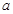 ,使得对任意
,使得对任意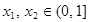 ,都有
,都有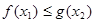 成立?
成立?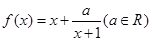 .
.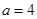 时,解不等式:
时,解不等式: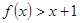 ;
;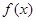 在
在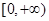 的最小值;
的最小值;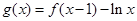 的单调递增区间.
的单调递增区间.