题目内容
已知正三角形内切圆的半径r与它的高h的关系是:r=
h,把这个结论推广到空间正四面体,则正四面体内切球的半径r与正四面体高h的关系是______.
| 1 |
| 3 |
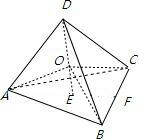
球心到正四面体一个面的距离即球的半径r,连接球心与正四面体的四个顶点.
把正四面体分成四个高为r的三棱锥,所以4×
S×r=
×S×h,
所以r=
h(其中S为正四面体一个面的面积,h为正四面体的高)
故答案为:r=
h.
把正四面体分成四个高为r的三棱锥,所以4×
| 1 |
| 3 |
| 1 |
| 3 |
所以r=
| 1 |
| 4 |
故答案为:r=
| 1 |
| 4 |


练习册系列答案
相关题目

 ,则( )
,则( )


