题目内容
已知M(-2,0),N(2,0),则以MN为斜边的直角三角形的直角顶点P的轨迹方程为( )
| A.x2+y2=2 | B.x2+y2=4 |
| C.x2+y2=2(x≠±2) | D.x2+y2=4(x≠±2) |
D
解析

练习册系列答案
相关题目
直线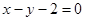 被圆
被圆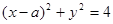 截得的弦长为
截得的弦长为 ,则实数
,则实数 的值为 ( )
的值为 ( )
A. 或 或 | B. 或 或 | C. 或 或 | D. 或 或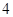 |
圆 上的点到直线
上的点到直线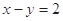 的距离最大值是( )
的距离最大值是( )
A. | B.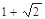 | C.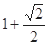 | D.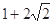 |
若直线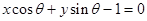 与圆
与圆 相切,且
相切,且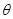 为锐角,则这条直线的斜率是( )
为锐角,则这条直线的斜率是( )
A.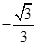 | B.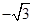 | C. | D.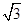 |
直线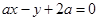 与圆
与圆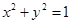 的位置关系是( )
的位置关系是( )
| A.相离 | B.相交 | C.相切 | D.不确定 |
若直线ax+by=1过点M(cos α,sin α),则( )
| A.a2+b2≥1 | B.a2+b2≤1 |
C.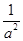 + +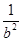 ≤1 ≤1 | D.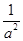 + +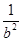 ≥1 ≥1 |
若点P(3,-1)为圆(x-2)2+y2=25的弦AB的中点,则直线AB的方程为( )
| A.x+y-2=0 | B.2x-y-7=0 |
| C.2x+y-5=0 | D.x-y-4=0 |
若圆O的半径为3,直径AB上一点D使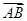 =3
=3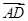 ,E、F为另一直径的两个端点,则
,E、F为另一直径的两个端点,则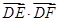 =( )
=( )
| A.-3 | B.-4 | C.-6 | D.-8 |
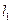 :
: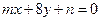 和
和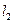 :
: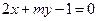 ,
,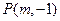 ,求
,求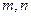 的值;
的值;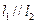 ,试确定
,试确定