题目内容
从装有2个黑球和2个白球的口袋内任取2个球，那么互斥而对立的两个事件是（ ）
| A．至少有1个黑球，至少有1个白球 | B．恰有1个黑球，恰有2个白球 |
| C．至少有1个黑球，都是黑球 | D．至少有1个黑球，都是白球 |
D
试题分析：根据题意，对于选项A至少有1个黑球，至少有1个白球，，“至少有一个黑球”，黑球的个数可能是1或2，表明红球个数为0或1，这与“至少有1个红球”不互斥，因此它们不对立；对于选项B，由于恰有1个黑球，恰有2个白球，互斥，但不是必有一个发生，故不对立，对于选项C，由于C.至少有1个黑球，都是黑球，可以同时发生，因此不互斥，对于D,由于至少一个黑球和没有黑球是对立事件，因此说至少有1个黑球，都是白球是对立事件，故选D.
点评：本题考查了随机事件当中“互斥”与“对立”的区别与联系，属于基础题
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
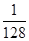
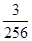
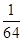
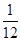
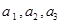，女生2名，记为
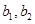，现从中任选2名学生去参加校数学竞赛
，黄球的概率为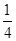
，袋中红球有4个，则袋中蓝球的个数为（ ）.
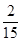B. 
C. 
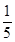D.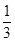 
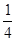
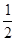
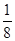
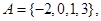在平面直角坐标系中，点
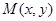的横、纵坐标满足
。
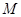的所有坐标；
轴上的概率；
上的概率。