题目内容
(本题满分12分)
已知集合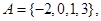 在平面直角坐标系中,点
在平面直角坐标系中,点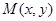 的横、纵坐标满足
的横、纵坐标满足 。
。
(1)请列出点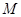 的所有坐标;
的所有坐标;
(2)求点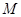 不在
不在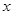 轴上的概率;
轴上的概率;
(3)求点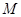 正好落在区域
正好落在区域 上的概率。
上的概率。
已知集合
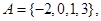 在平面直角坐标系中,点
在平面直角坐标系中,点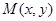 的横、纵坐标满足
的横、纵坐标满足 。
。(1)请列出点
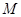 的所有坐标;
的所有坐标;(2)求点
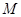 不在
不在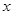 轴上的概率;
轴上的概率;(3)求点
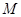 正好落在区域
正好落在区域 上的概率。
上的概率。(1)(-2,-2),(-2,0),(-2,1),(-2,3);(0,-2),(0,0),(0,1),(0,3);
(1,-2),(1,0),(1,1),(1,3);(3,-2),(3,0),(3,1),(3,3)
(2)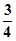 (3)
(3)
(1,-2),(1,0),(1,1),(1,3);(3,-2),(3,0),(3,1),(3,3)
(2)
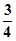 (3)
(3)
试题分析:(1)
 集合
集合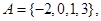 点
点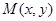 的横、纵坐标满足
的横、纵坐标满足 ,
, 点
点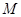 的坐标共有:
的坐标共有: 个,分别是:
个,分别是:(-2,-2),(-2,0),(-2,1),(-2,3);(0,-2),(0,0),(0,1),(0,3);
(1,-2),(1,0),(1,1),(1,3);(3,-2),(3,0),(3,1),(3,3)……4分
(2)点
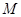 不在
不在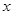 轴上的坐标共有12种:
轴上的坐标共有12种:(-2,-2),(0,-2),(-2,1),(-2,3);(1,-2),(0,1),(1,1),(1,3);
(3,-2),(0,3),(3,1),(3,3)
所以点
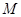 不在
不在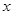 轴上的概率是
轴上的概率是 ……8分
……8分(3)点
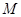 正好落在区域
正好落在区域 上的坐标共有3种:(1,1),(1,3),(3,1)
上的坐标共有3种:(1,1),(1,3),(3,1)故
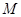 正好落在该区域上的概率为
正好落在该区域上的概率为 ……12分
……12分点评:古典概率需要找到所有基本事件总数及满足某一条件的基本事件数目,然后求其比值

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目

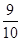
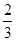
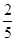
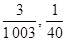

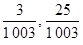

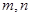 作为点
作为点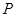 的坐标,则点
的坐标,则点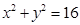 内的概率为( )
内的概率为( )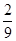
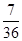
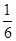
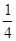
 张卡片(大小,形状都相同)上分别写有
张卡片(大小,形状都相同)上分别写有 ,
, ,
,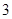 ,
,