ЬтФПФкШн
ЁОЬтФПЁПФГбЇаЃбаОПадбЇЯАаЁзщЖдИУаЃИпШ§бЇЩњЪгСІЧщПіНјааЕїВщЃЌдкИпШ§ЕФШЋЬх1000УћбЇЩњжаЫцЛњГщШЁСЫ100УћбЇЩњЕФЬхМьБэЃЌВЂЕУЕНШчЭМЕФЦЕТЪЗжВМжБЗНЭМ.
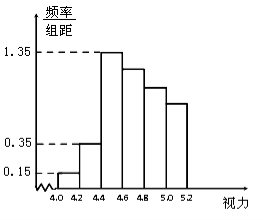
ЃЈ1ЃЉШєжБЗНЭМжаКѓЫФзщЕФЦЕЪ§ГЩЕШВюЪ§СаЃЌЪдЙРМЦШЋФъМЖЪгСІдк5.0вдЯТЕФШЫЪ§ЃЛ
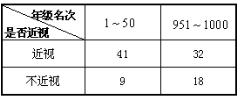
ЃЈ2ЃЉбЇЯАаЁзщГЩдБЗЂЯжЃЌбЇЯАГЩМЈЭЛГіЕФбЇЩњЃЌНќЪгЕФБШНЯЖрЃЌЮЊСЫбаОПбЇЩњЕФЪгСІгыбЇЯАГЩМЈЪЧЗёгаЙиЯЕЃЌЖдФъМЖУћДЮдк1ЁЋ50УћКЭ951ЁЋ1000УћЕФбЇЩњНјааСЫЕїВщЃЌЕУЕНгвБэжаЪ§ОнЃЌИљОнБэжаЕФЪ§ОнЃЌФмЗёдкЗИДэЕФИХТЪВЛГЌЙ§0.05ЕФЧАЬсЯТШЯЮЊЪгСІгыбЇЯАГЩМЈгаЙиЯЕ?
ЃЈ3ЃЉдкЃЈ2ЃЉжаЕїВщЕФ100УћбЇЩњжаЃЌАДееЗжВуГщбљдкВЛНќЪгЕФбЇЩњжаГщШЁСЫ9ШЫЃЌНјвЛВНЕїВщЫћУЧСМКУЕФЛЄблЯАЙпЃЌВЂЧвдкет9ШЫжаШЮШЁ3ШЫЃЌМЧУћДЮдк1ЁЋ50ЕФбЇЩњШЫЪ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ИНЃК

![]()
ЁОД№АИЁПЃЈ1ЃЉ820ШЫЃЛЃЈ2ЃЉдкЗИДэЮѓЕФИХТЪВЛГЌЙ§0.05ЕФЧАЬсЯТШЯЮЊЪгСІгыбЇЯАГЩМЈгаЙиЯЕЃЛЃЈ3ЃЉЗжВМСаМћНтЮіЃЌЦкЭћЮЊ1ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЦЕТЪПЩМЦЫуГіЧАШ§зщЕФЦЕЪ§ЃЌШЛКѓРћгУКѓЫФзщЦЕЪ§ГЩЕШВюЪ§СаПЩЕУКѓЫФзщЕФЦЕЪ§ДгЖјЕУГібљБОжаЪгСІдк5.0вдЯТЕФШЫЪ§ЃЌдйЕУГіШЋФъМЖЪгСІдк5.0вдЯТЕФШЫЪ§ЃЛЃЈ2ЃЉгЩЫљИј![]() ЙЋЪНМЦЫуГі
ЙЋЪНМЦЫуГі![]() КѓЃЌгыЫљИјЪ§ОнБШНЯПЩЕУЯрЙиадЃЛЃЈ3ЃЉвРЬтвт9ШЫжаФъМЖУћДЮдк1ЁЋ50УћКЭ951ЁЋ1000УћЗжБ№га3ШЫКЭ6ШЫЃЌ
КѓЃЌгыЫљИјЪ§ОнБШНЯПЩЕУЯрЙиадЃЛЃЈ3ЃЉвРЬтвт9ШЫжаФъМЖУћДЮдк1ЁЋ50УћКЭ951ЁЋ1000УћЗжБ№га3ШЫКЭ6ШЫЃЌ
![]() ПЩШЁ0ЁЂ1ЁЂ2ЁЂ3ЃЌгЩЙХЕфИХаЭИХТЪЙЋЪНПЩМЦЫуГіУћЪТМўИХТЪЃЌЕУИХТЪЗжВМСаЃЌдђЪ§бЇЦкЭћЙЋЪНПЩМЦЫуГіЦкЭћЃЎ
ПЩШЁ0ЁЂ1ЁЂ2ЁЂ3ЃЌгЩЙХЕфИХаЭИХТЪЙЋЪНПЩМЦЫуГіУћЪТМўИХТЪЃЌЕУИХТЪЗжВМСаЃЌдђЪ§бЇЦкЭћЙЋЪНПЩМЦЫуГіЦкЭћЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЩшИїзщЕФЦЕТЪЮЊ![]() ЃЌ
ЃЌ
гЩЭМПЩжЊЃЌЕквЛзщга3ШЫЃЌЕкЖўзщ7ШЫЃЌЕкШ§зщ27ШЫЃЌ
вђЮЊКѓЫФзщЕФЦЕЪ§ГЩЕШВюЪ§СаЃЌ
ЫљвдКѓЫФзщЦЕЪ§вРДЮЮЊ![]()
ЫљвдЪгСІдк5.0вдЯТЕФЦЕТЪЮЊ3+7+27+24+21=82ШЫЃЌ
ЙЪШЋФъМЖЪгСІдк5.0вдЯТЕФШЫЪ§дМЮЊ![]()
ЃЈ2ЃЉ![]()
вђДЫдкЗИДэЮѓЕФИХТЪВЛГЌЙ§0.05ЕФЧАЬсЯТШЯЮЊЪгСІгыбЇЯАГЩМЈгаЙиЯЕ.
ЃЈ3ЃЉвРЬтвт9ШЫжаФъМЖУћДЮдк1ЁЋ50УћКЭ951ЁЋ1000УћЗжБ№га3ШЫКЭ6ШЫЃЌ![]() ПЩШЁ0ЁЂ1ЁЂ2ЁЂ3
ПЩШЁ0ЁЂ1ЁЂ2ЁЂ3
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]()
![]() ЕФЗжВМСаЮЊ
ЕФЗжВМСаЮЊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() ЕФЪ§бЇЦкЭћ
ЕФЪ§бЇЦкЭћ![]()

ЁОЬтФПЁПЙлВьЯТБэЃК
x | Ѓ3 | Ѓ2 | Ѓ1 | 1 | 2 | 3 |
fЃЈxЃЉ | 5 | 1 | Ѓ1 | Ѓ3 | 3 | 5 |
gЃЈxЃЉ | 1 | 4 | 2 | 3 | Ѓ2 | Ѓ4 |
дђf[gЃЈ3ЃЉЃfЃЈЃ1ЃЉ]ЃН ЃЈ ЃЉ
A.3
B.4
C.Ѓ3
D.5
