题目内容
已知曲线C的方程是(t+1) +2at)x+3at+b=0,直线l的
+2at)x+3at+b=0,直线l的
方程是y=t(x-1),若对任意实数t,曲线C恒过定点P(1,0).
(1)求定值a,b;
(2)直线l截曲线C所得弦长为d,记f(t)= ,则当t为何值时,f(t)有最大值,最大值是多少?
,则当t为何值时,f(t)有最大值,最大值是多少?
(3)若点M( )在曲线C上,又在直线l上,求
)在曲线C上,又在直线l上,求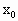 的取值范围.
的取值范围.
答案:
解析:
解析:
|
解:(1)∵曲线C恒过定点P(1,0),∴(t+1)-2( ∴a=1,b=1. (2)由(1)知曲线C为:(t+1) 以y=t(x-1)代入得( ∴ ∴f(t)= 当t>0时,|t+ 当t<0时,t+ 综上讨论: (3)由题设知 当( |

练习册系列答案
相关题目
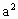 +2at)+3at+b=0恒成立,即(1-a)t+1-
+2at)+3at+b=0恒成立,即(1-a)t+1-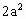 +b=0恒成立,
+b=0恒成立,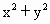 -2(1+2t)x+3t+1=0,
-2(1+2t)x+3t+1=0,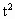 +t+1)
+t+1)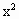 -
- +3t+1=0(*),
+3t+1=0(*),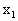 =1,
=1,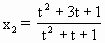 ,∴d=
,∴d=
 ,
,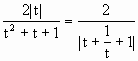 .(t≠0,否则y=0,f(t)=0)
.(t≠0,否则y=0,f(t)=0)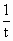 +1|=t+
+1|=t+ ;
;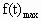 =2,这时t=-1.
=2,这时t=-1. 是方程(*)的解,∴
是方程(*)的解,∴ =1或
=1或 ,
,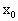 -1)
-1)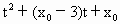 -1=0,
-1=0,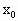 ≠1时必须有Δ=
≠1时必须有Δ= =
=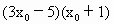 ≤0.∴
≤0.∴