题目内容
(2012•西城区二模)已知曲线C的方程是(x-
)2+(y-
)2=8,给出下列三个结论:
①曲线C与两坐标轴有公共点;
②曲线C既是中心对称图形,又是轴对称图形;
③若点P,Q在曲线C上,则|PQ|的最大值是6
.
其中,所有正确结论的序号是
| |x| |
| x |
| |y| |
| y |
①曲线C与两坐标轴有公共点;
②曲线C既是中心对称图形,又是轴对称图形;
③若点P,Q在曲线C上,则|PQ|的最大值是6
| 2 |
其中,所有正确结论的序号是
②③
②③
.分析:先分类讨论化简方程,再根据方程对应轭曲线,即可得到结论.
解答: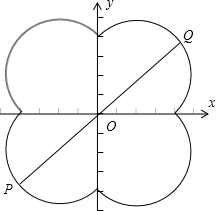 解:当x>0,y>0时,方程是(x-1)2+(y-1)2=8;
解:当x>0,y>0时,方程是(x-1)2+(y-1)2=8;
当 x>0,y<0 时,方程是(x-1)2+(y+1)2=8;
当 x<0,y>0 时,方程是(x+1)2+(y-1)2=8;
当 x<0,y<0 时,方程是(x+1)2+(y+1)2=8
由于x≠0且y≠0,所以①不正确;
曲线C既是中心对称图形,又是轴对称图形,对称中心为(0,0),对称轴为x,y轴,故②正确;
点P,Q在曲线C上,当且仅当P,Q与圆弧所在圆心共线时取得最大值,|PQ|的最大值是圆心距加两个半径,即6
,故③正确.
综上知②③
故答案为:②③
 解:当x>0,y>0时,方程是(x-1)2+(y-1)2=8;
解:当x>0,y>0时,方程是(x-1)2+(y-1)2=8;当 x>0,y<0 时,方程是(x-1)2+(y+1)2=8;
当 x<0,y>0 时,方程是(x+1)2+(y-1)2=8;
当 x<0,y<0 时,方程是(x+1)2+(y+1)2=8
由于x≠0且y≠0,所以①不正确;
曲线C既是中心对称图形,又是轴对称图形,对称中心为(0,0),对称轴为x,y轴,故②正确;
点P,Q在曲线C上,当且仅当P,Q与圆弧所在圆心共线时取得最大值,|PQ|的最大值是圆心距加两个半径,即6
| 2 |
综上知②③
故答案为:②③
点评:本题考查曲线与方程的概念,体现分类讨论、数形结合的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•西城区二模)如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB.
(2012•西城区二模)如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB. (2012•西城区二模)执行如图所示的程序框图,若输入如下四个函数:
(2012•西城区二模)执行如图所示的程序框图,若输入如下四个函数: