题目内容
已知 为函数
为函数 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线 的斜率
的斜率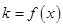 .
.
(Ⅰ)若函数 在区间
在区间
 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;
(Ⅱ)设 ,若对任意
,若对任意 恒有
恒有 ,求实数
,求实数 的取值范围.
的取值范围.
(Ⅰ)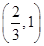 ;(Ⅱ)
;(Ⅱ)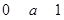 .
.
解析试题分析:(Ⅰ)根据斜率的定义写现 的表达式,并用导数探究其在区间
的表达式,并用导数探究其在区间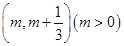 极值存在的条件.(Ⅱ)
极值存在的条件.(Ⅱ)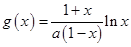 ,因为
,因为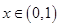 ,所以
,所以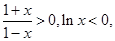 所以
所以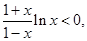
故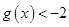 转化为
转化为 ,令
,令 ,借助导数研究函数
,借助导数研究函数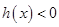 ,
,
的条件,求得实数 的取值范围.
的取值范围.
试题解析:(1)由题意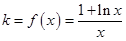 ,
,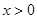 1分
1分
所以 2分
2分
当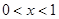 时,
时,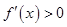 ;当
;当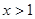 时,
时,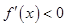 .所以
.所以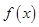 在
在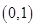 上单调递增,在
上单调递增,在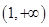 上单调递减,故
上单调递减,故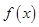 在
在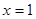 处取得极大值. 3分
处取得极大值. 3分
因为函数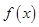 在区间
在区间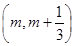 (其中
(其中 )上存在极值,
)上存在极值,
所以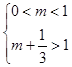 ,得
,得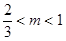 .即实数
.即实数 的取值范围是
的取值范围是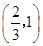 . 5分
. 5分
(Ⅱ)有题可知,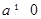 ,因为
,因为 ,所以
,所以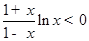 .当
.当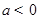 时,
时, 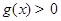 ,不合题意.当
,不合题意.当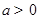 时,由
时,由 ,可得
,可得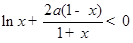 8分
8分
设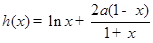 ,则
,则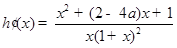 .
.
设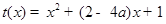 ,
,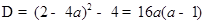 .
.
(1)若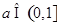 ,则
,则 ,
,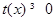 ,
,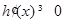 ,所以
,所以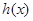 在
在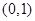 内单调递增,又
内单调递增,又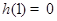 所以
所以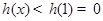 .所以
.所以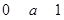 符合条件. 10分
符合条件. 10分
(2)若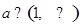 ,则
,则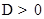 ,
,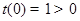 ,
,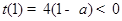 ,所以存在
,所以存在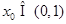 ,使得
,使得 ,对任意
,对任意 ,
,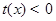 ,
,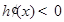 .则
.则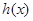 在
在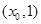 内单调递减,又
内单调递减,又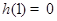 ,所以当
,所以当 时,
时,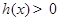

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 .若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格).
.若乙方每生产一吨产品必须赔付甲方S元(以下称S为赔付价格). .
. 在点
在点 处的切线与直线
处的切线与直线 平行,求实数
平行,求实数 的值;
的值; 在
在 处取得极小值,且
处取得极小值,且 ,求实数
,求实数 的取值范围.
的取值范围. .
. ,求
,求 的最小值;
的最小值; 的图象,使得
的图象,使得 的图象有公共点且在公共点处切线相同.
的图象有公共点且在公共点处切线相同. 的正方形
的正方形 内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为
内建一个交通“环岛”.正方形的四个顶点为圆心在四个角分别建半径为 (
( 不小于
不小于 )的扇形花坛,以正方形的中心为圆心建一个半径为
)的扇形花坛,以正方形的中心为圆心建一个半径为 的圆形草地.为了保证道路畅通,岛口宽不小于
的圆形草地.为了保证道路畅通,岛口宽不小于 ,绕岛行驶的路宽均不小于
,绕岛行驶的路宽均不小于 .
.
 取
取 )
) 元
元 ,四个花坛的造价为
,四个花坛的造价为 元
元 元
元 ,函数
,函数 .
. 时,求
时,求 的最小值;
的最小值; 上是单调函数,求
上是单调函数,求 的取值范围.
的取值范围. ,其中
,其中
 是自然对数的底数.
是自然对数的底数. 的零点;
的零点;
 均有两个极值点,一个在区间
均有两个极值点,一个在区间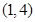 内,另一个在区间
内,另一个在区间 外,
外, 的取值范围;
的取值范围; 且函数
且函数 在
在 上是单调函数,探究函数
上是单调函数,探究函数 的单调性.
的单调性. ,其中
,其中 ,曲线
,曲线 在点
在点 处的切线垂直于
处的切线垂直于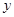 轴.
轴. 的值;
的值; 的极值.
的极值.