题目内容
已知 ,函数
,函数 .
.
(Ⅰ)当 时,求
时,求 的最小值;
的最小值;
(Ⅱ)若 在区间
在区间 上是单调函数,求
上是单调函数,求 的取值范围.
的取值范围.
(Ⅰ)1;(Ⅱ) 或
或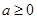
解析试题分析:(Ⅰ)先求导再讨论其单调性,根据单调性可求其最值。(Ⅱ) 在区间
在区间 上是单调函数说明在
上是单调函数说明在 上
上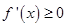 或
或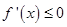 恒成立。
恒成立。 的取值范围应将函数单调性问题转化为求最值问题。注意对
的取值范围应将函数单调性问题转化为求最值问题。注意对 的讨论。
的讨论。
试题解析:解:(Ⅰ)当 时,
时,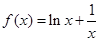 (
(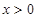 ),
),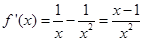 .
.
所以,当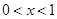 时,
时,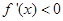 ;当
;当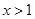 时,
时, .
.
所以,当 时,函数有最小值
时,函数有最小值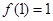 . 6分
. 6分
(Ⅱ)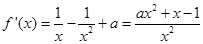 .
.
当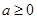 时,
时, 在
在 上恒大于零,即
上恒大于零,即 ,符合要求.
,符合要求.
当 时,要使
时,要使 在区间
在区间 上是单调函数,
上是单调函数,
当且仅当 时,
时, 恒成立.
恒成立.
即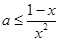 恒成立.
恒成立.
设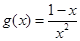 ,
,
则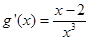 ,
,
又 ,所以
,所以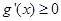 ,即
,即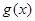 在区间
在区间 上为增函数,
上为增函数,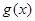 的最小值为
的最小值为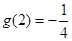 ,所以
,所以 .
.
综上,  的取值范围是
的取值范围是 ,或
,或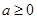 . 13分
. 13分
考点:1导数;2利用导数研究函数性质。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
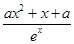 .
.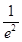 恒成立,求a的取值范围.
恒成立,求a的取值范围. .
.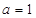 ,求函数
,求函数 的单调区间和极值;
的单调区间和极值; 的斜率为
的斜率为 ,当
,当 为函数
为函数 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线 的斜率
的斜率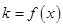 .
. 在区间
在区间
 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围; ,若对任意
,若对任意 恒有
恒有 ,求实数
,求实数 的取值范围.
的取值范围. ,货车从甲地匀速行驶到乙地,速度不得超过80
,货车从甲地匀速行驶到乙地,速度不得超过80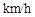 ,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的
,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的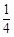 倍,固定成本为a元.
倍,固定成本为a元. .
. ,求
,求 在点
在点 处的切线方程;
处的切线方程; 恒成立,求
恒成立,求 的取值范围.
的取值范围.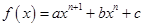
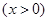 ,其中
,其中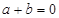 ,
,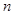 为正整数,
为正整数, 、
、 、
、 均为常数,曲线
均为常数,曲线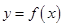 在
在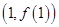 处的切线方程为
处的切线方程为 .
.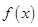 的最大值;
的最大值;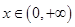 都有
都有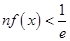 .(
.(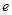 为自然对数的底)
为自然对数的底) ,
, .
. 与
与 在
在 处相切,试求
处相切,试求 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;

 .
. 的一个极值点。
的一个极值点。 在区间
在区间 上单调递减,求实数m的取值范围;
上单调递减,求实数m的取值范围; ,对于任意
,对于任意 和
和 ,有不等式
,有不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.