题目内容
【题目】已知等比数列{an},a1=1,a6=32,Sn是等差数列{bn}的前n项和,b1=3,S5=35.
(1)求数列{an},{bn}的通项公式;
(2)设cn=an+bn , 求数列{cn}的前n项和Tn .
【答案】
(1)解:设{an}的公比为q,则 ![]() ,
,
即q5=32,∴q=2, ![]() .
.
设{bn}的公差为d,则 ![]() ,即15+10d=35,解得d=2,
,即15+10d=35,解得d=2,
∴bn=3+(n﹣1)×2=2n+1
(2)解:设{an}的前n项和为An,
则An= ![]() =
= ![]() =2n﹣1,
=2n﹣1,
Sn=nb1+ ![]() =3n+
=3n+ ![]() =n2+2n,
=n2+2n,
∵cn=an+bn,
∴Tn=An+Sn=2n+n2+2n﹣1
【解析】(1)列方程求出{an}的公比和{bn}的公差,即可得出其通项公式;(2)分别求出{an}和{bn}的前n项和,将两数列的前n项和相加即为Tn .
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系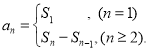 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至11月份销售某种机械配件的销售量及销售单价进行了调查,销售单价x元和销售量y件之间的一组数据如表所示:
月份 | 7 | 8 | 9 | 10 | 11 |
销售单价x元 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y件 | 11 | 10 | 8 | 6 | 5 |
(1)根据7至11月份的数据,求出y关于x的回归直线方程;
(2)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润? 参考公式:回归直线方程 ![]() =b
=b ![]() +a,其中b=
+a,其中b= 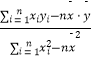 .
.
参考数据: ![]() =392,
=392, ![]() =502.5.
=502.5.