题目内容
(2010•天津模拟)已知区域M={(x,y)||x|+|y-2|≤2,x,y∈R},则区域M内的点到坐标原点的距离不超过2的概率是
.
| π |
| 8 |
| π |
| 8 |
分析:本题利用几何概型计算,试验包含的所有事件是区域D表示边长为2
的正方形的内部(含边界),满足条件的事件表示圆及其内部,根据几何概型概率公式得到结果.
| 2 |
解答: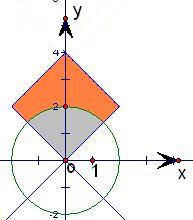 解:|x|+|y-2|≤2?
解:|x|+|y-2|≤2?
或
或
或
,分别画出它们所表示的平面区域得,
区域M={(x,y)||x|+|y-2|≤2,x,y∈R}表示的平面区域是一个正方形,边长为2
.其图形如图中阴影部分,
∴试验包含的所有事件是区域M表示边长为2
的正方形的内部(含边界),面积是(2
)2=8,
满足条件的事件表示半径为2圆的在正方形区域内部的部分,是四分之一个圆,面积是
×π×22
根据几何概型概率公式得到
∴P=
故答案为:
.
 解:|x|+|y-2|≤2?
解:|x|+|y-2|≤2?
|
|
|
|
区域M={(x,y)||x|+|y-2|≤2,x,y∈R}表示的平面区域是一个正方形,边长为2
| 2 |
∴试验包含的所有事件是区域M表示边长为2
| 2 |
| 2 |
满足条件的事件表示半径为2圆的在正方形区域内部的部分,是四分之一个圆,面积是
| 1 |
| 4 |
根据几何概型概率公式得到
∴P=
| π |
| 8 |
故答案为:
| π |
| 8 |
点评:本题考查几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到,本题是通过两个图形的面积之比得到概率的值.本题可以以选择和填空形式出现.

练习册系列答案
相关题目
 (2010•天津模拟)某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是
(2010•天津模拟)某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是