题目内容
已知某车站每天8：00—9：00、9：00—10：00都恰好有一辆客车到站；8：00—9：00到站的客车A可能在8：10、8：30、8：50到，其概率依次为16,12，13.9：00—10：00到站的客车B可能在9：10、9：30、9：50到，其概率依次为16,12,13.今有甲、乙两位旅客，他们到站的时间分别为8：00和8：20，甲旅客选择A车，乙旅客可选A或B车，试问他们候车时间的平均值哪个更多？
解析：旅客甲候车时间的平均值比乙多.设甲、乙两位旅客的候车时间分别为ξ，η分钟，则他们的分布列为：
甲旅客
ξ | 10 | 30 | 50 |
p |
|
|
|
乙旅客
η | 10 | 30 | 50 | 70 | 90 |
P |
|
|
|
|
|
·
·
·
易知Eξ=10×
+30×
+50×
=
,Eη=10×
+30×
+50×
+70×
+90×
,Eξ＞Eη,旅客甲候车时间的平均值比乙多.
练习册系列答案
相关题目
可能在8：10、8：30、8：50到，其概率依次为
．9：00―10：00到站的客车
可能在9：10、9：30、9：50到，其概率依次为
,
,
;9:00—10:00到站的客车可能在9:10,9:30和9:50到站,其概率依次为
,
,
.今有甲、乙两位旅客要从A地到B地,他们到达车站的时间分别是8:00和8:20,假设只要有车到站就一定能坐上车,设甲与乙的候车时间分别为ξ分钟和η分钟.
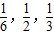；9：00～10：00到站的客车B可能在9：10，9：30，9：50到站，其概率依次为
．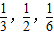