题目内容
某车站每天8:00~9:00,9:00~10:00都恰有一辆客车到站,8:00~9:00到站的客车A可能在8:10,8:30,8:50到站,其概率依次为
,
,
;9:00~10:00到站的客车B可能在9:10,9:30,9:50到站,其概率依次为
,
,
.
(1)旅客甲8:00到站,设他的候车时间为ξ,求ξ的分布列和Eξ;
(2)旅客乙8:20到站,设他的候车时间为η,求η的分布列和Eη.
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
(1)旅客甲8:00到站,设他的候车时间为ξ,求ξ的分布列和Eξ;
(2)旅客乙8:20到站,设他的候车时间为η,求η的分布列和Eη.
分析:(1)旅客8:00到站,他的候车时间ξ的取值可能为10,30,50,P(ξ=10)=
,P(ξ=30)=
,P(ξ=50)=
,由此能求出ξ的分布列和Eξ.
(2)旅客乙8:20到站,他的候车时间η的取值可能为10,30,50,70,90,P(η=10)=
,P(η=30)=
,P(η=50)=
×
=
,P(η=70)=
×
=
,P(η=90)=
×
=
.由此能求出η的分布列和Eη.
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
(2)旅客乙8:20到站,他的候车时间η的取值可能为10,30,50,70,90,P(η=10)=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 18 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 12 |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 36 |
解答:解:(1)旅客8:00到站,他的候车时间ξ的取值可能为10,30,50,
P(ξ=10)=
,
P(ξ=30)=
,
P(ξ=50)=
,
∴ξ的分布列为:
∴Eξ=10×
+30×
+50×
=
(分钟)
(2)旅客乙8:20到站,他的候车时间η的取值可能为10,30,50,70,90,
P(η=10)=
P(η=30)=
,
P(η=50)=
×
=
,
P(η=70)=
×
=
,
P(η=90)=
×
=
.
η的分布列为:
∴Eη=10×
+30×
+50×
+70×
+90×
=
(分钟)
P(ξ=10)=
| 1 |
| 6 |
P(ξ=30)=
| 1 |
| 2 |
P(ξ=50)=
| 1 |
| 3 |
∴ξ的分布列为:
| ζ | 10 | 30 | 50 | ||||||
| P |
|
|
|
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 100 |
| 3 |
(2)旅客乙8:20到站,他的候车时间η的取值可能为10,30,50,70,90,
P(η=10)=
| 1 |
| 2 |
P(η=30)=
| 1 |
| 3 |
P(η=50)=
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 18 |
P(η=70)=
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 12 |
P(η=90)=
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 36 |
η的分布列为:
| η | 10 | 30 | 50 | 70 | 90 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 18 |
| 1 |
| 12 |
| 1 |
| 36 |
| 235 |
| 9 |
点评:本题考查离散型随机变量的分布列和数学期望,是基础题.解题时要认真审题,仔细解答,注意概率知识的合理运用.

练习册系列答案
相关题目
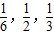 ;9:00~10:00到站的客车B可能在9:10,9:30,9:50到站,其概率依次为
;9:00~10:00到站的客车B可能在9:10,9:30,9:50到站,其概率依次为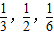 .
.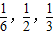 ;9:00~10:00到站的客车B可能在9:10,9:30,9:50到站,其概率依次为
;9:00~10:00到站的客车B可能在9:10,9:30,9:50到站,其概率依次为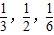 .
.