题目内容
15.已知函数f(x)=4sin2(x+$\frac{π}{4}$)-2$\sqrt{3}$cos2x+1,且给定条件p:$\frac{π}{4}$≤x≤$\frac{π}{2}$,又给定条件q:|f(x)-m|<2,且p是q的充分条件,则实数m的取值范围是( )| A. | (-2,2) | B. | (5,7) | C. | (3,5) | D. | (1,3) |
分析 先根据两角和与差的公式进行化简,再由x的范围求出2x-$\frac{π}{3}$的范围,再结合正弦函数的性质可求出m的范围,再根据|f(x)-m|<2求出f(x)的范围,再由p是q的充分条件和(1)中f(x)的最大、最小值可得到m的范围即可.
解答 解:∵f(x)=2[1-cos($\frac{π}{2}$+2x)]-2$\sqrt{3}$cos2x+1
=2sin2x-2$\sqrt{3}$cos2x+3
=4sin(2x-$\frac{π}{3}$)+3.
又∵$\frac{π}{4}$≤x≤$\frac{π}{2}$,
∴$\frac{π}{6}$≤2x-$\frac{π}{3}$≤$\frac{2π}{3}$,
即5≤4sin(2x-$\frac{π}{3}$)+3≤7,
∴f(x)max=7,f(x)min=5,
∴P:m∈[5,7];
∵|f(x)-m|<2,
∴m-2<f(x)<m+2
又p是q的充分条件
∵$\left\{\begin{array}{l}{m-2<5}\\{m+2>7}\end{array}\right.$,
∴5<m<7.
故选:B.
点评 本题主要考查两角和与差的公式的应用和正弦函数的性质.高考中对三角函数的考查以基础题为主,平时要注意对基础知识的积累和运用的灵活性的锻炼.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
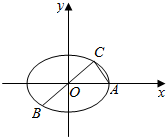 已知A,B,C是椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$上的不同三点,其中点A的坐标为(2$\sqrt{3}$,0),BC过椭圆的中心,点C在第一象限,且满足∠BAC=90°,|BC|=2|AC|.
已知A,B,C是椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$上的不同三点,其中点A的坐标为(2$\sqrt{3}$,0),BC过椭圆的中心,点C在第一象限,且满足∠BAC=90°,|BC|=2|AC|.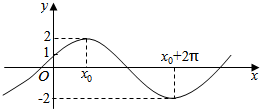 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象与y轴的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点的坐标分别为(x0,2)和(x0+2π,-2).