题目内容
定义在 上的函数
上的函数 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列 ,
,  仍是等比数列,则称
仍是等比数列,则称 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在 上的如下函数:①
上的如下函数:① ; ②
; ②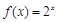 ; ③
; ③ ; ④
; ④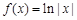 .
.
则其中是“保等比数列函数”的 的序号为 ( )
的序号为 ( )
A①② B.③④ C.①③ D.②④
C
解析试题分析:根据新定义,结合等比数列性质 ,则在①
,则在① ,那么可知
,那么可知 ,故正确
,故正确
对于②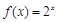 ,
, ,故不正确
,故不正确
③ ;
; ,故正确
,故正确
④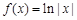 ,
, ,故不正确,故选C
,故不正确,故选C
考点:等比数列
点评:本题考查等比数列性质及函数计算,正确运算,理解新定义是解题的关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数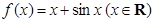 ( )
( )
A.是偶函数,且在 上是减函数 上是减函数 | B.是偶函数,且在 上是增函数 上是增函数 |
C.是奇函数,且在 上是减函数 上是减函数 | D.是奇函数,且在 上是增函数 上是增函数 |
已知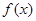 为定义在
为定义在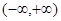 上的可导函数,且
上的可导函数,且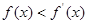 对于任意
对于任意 恒成立,则( )
恒成立,则( )
A.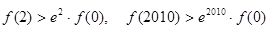 |
B.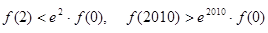 |
C.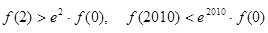 |
D.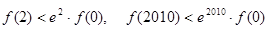 |
函数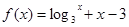 零点所在大致区间是( )
零点所在大致区间是( )
| A.(1,2) | B.(2,3) | C.(3,4) | D.(4,5) |
函数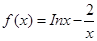 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A.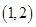 | B.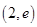 |
C. | D.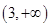 |
设 ,用二分法求方程
,用二分法求方程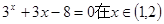 内近似解的过程
内近似解的过程
中得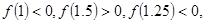 则方程的根落在区间
则方程的根落在区间
A.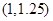 | B. | C.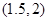 | D.不能确定 |
设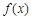 在
在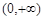 上是单调递增函数,当
上是单调递增函数,当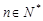 时,
时,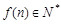 ,且
,且 ,则( )
,则( )
A.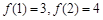 | B. |
C.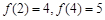  | D.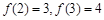 |
下列函数在区间[0, ]上是减函数的是
]上是减函数的是
| A.y="sin" x | B.y="cos" x | C.y="tan" x | D.y=2 |
函数 ( )
( )
A.是奇函数,且在 上是单调增函数 上是单调增函数 |
B.是奇函数,且在 上是单调减函数 上是单调减函数 |
C.是偶函数,且在 上是单调增函数 上是单调增函数 |
D.是偶函数,且在 上是单调减函数 上是单调减函数 |