题目内容
【题目】设椭圆
的焦点分别为
、
，直线
：
交
轴于点
，且
（1）求椭圆的方程；
（2）过
分别作互相垂直的两直线
，与椭圆分别交于D、E和M、N四点， 求四边形
面积的最大值和最小值．
【答案】（1）
；（2）最大值为4，最小值为
.
【解析】
(1)根据
解得a，再根据c=1解得b,(2)先考虑
斜率不存在时四边形
的面积，再考虑
斜率存在时，利用韦达定理求弦长，再利用面积公式求四边形面积，最后根据基本不等式求最值.
（1）因为 ，所以
.
（2）当直线
与
轴垂直时，
，此时
，四边形的面积
．同理当
与轴垂直时，四边形的面积．
当直线，均与轴不垂直时，设
，代入椭圆方程消去
得：
设
所以
同理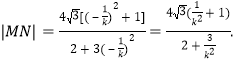
所以四边形的面积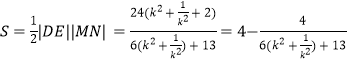
因为
，所以
．
综上可知，
．故四边形面积的最大值为4，最小值为．
阅读快车系列答案【题目】为了培养学生的安全意识，某中学举行了一次“安全自救”的知识竞赛活动，共有800名学生参加了这次竞赛.为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，得到如下的频率分布表，请你根据频率分布表解答下列问题：
序号（i） | 分组（分数） | 组中值（Gi） | 频数（人数） | 频率（fi） |
1 |
| 65 | ① | 0.10 |
2 |
| 75 | 20 | ② |
3 |
| 85 | ③ | 0.20 |
4 |
| 95 | ④ | ⑤ |
合计 | 50 | 1.00 | ||
（1）求出频率分布表中①②③④⑤处的值；
（2）为鼓励更多的学生了解“安全自救”知识，成绩不低于85分的学生能获奖，请估计在参加的800名学生中大约有多少名学生能获奖；
（3）求这800名学生的平均分.
【题目】数学是研究数量、结构、变化、空间以及信息等概念的一门科学.在人类历史发展和社会生活中，数学发挥着不可替代的作用，也是学习和研究现代科学技术必不可少的基本工具.
（1）为调查大学生喜欢数学命题是否与性别有关，随机选取
名大学生进行问卷调查，当被调查者问卷评分不低于
分则认为其喜欢数学命题，当评分低于分则认为其不喜欢数学命题，问卷评分的茎叶图如下：
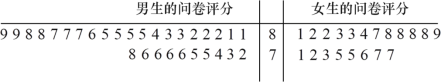
依据上述数据制成如下列联表：
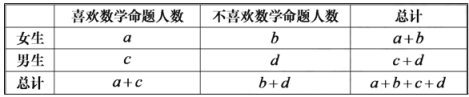
请问是否有
的把握认为大学生是否喜欢数学命题与性别有关？
参考公式及数据：
.
|
|
|
|
|
|
|
|
|
|
（2）在某次命题大赛中，
同学要进行
轮命题，其在每轮命题成功的概率均为
，各轮命题相互独立，若该同学在
轮命题中恰有
次成功的概率为
，记该同学在轮命题中的成功次数为
，求
.