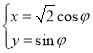题目内容
【题目】已知数列![]() ,
,![]() ,
,![]() 的前n项和为
的前n项和为![]() .
.
(1)若![]() ,
,![]() ,求证:
,求证:![]() ,其中
,其中![]() ,
,![]() ;
;
(2)若对任意![]() 均有
均有![]() ,求
,求![]() 的通项公式;
的通项公式;
(3)若对任意![]() 均有
均有![]() ,求证:
,求证:![]() .
.
【答案】(1)证明见解析 ;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)求出数列的通项公式,代入所证明的不等式转化求解即可;
(2)利用递推关系,说明![]() 是首项为
是首项为![]() ,公比为3的等比数列,然后求解即可;
,公比为3的等比数列,然后求解即可;
(3)化简数列的递推关系式,得出![]() 是首项为1,公差为1的等差数列,求出
是首项为1,公差为1的等差数列,求出![]() 的通项公式,用倒序相加法求数列的前
的通项公式,用倒序相加法求数列的前![]() 项和,利用(1)结论进行放缩,然后证明即可.
项和,利用(1)结论进行放缩,然后证明即可.
解:(1)由已知![]() 为等差数列,且
为等差数列,且![]() ,
,

![]()
![]()
![]() ,
,
即![]()
![]()
![]() ;
;
(2)![]()
![]()
所以![]() 是首项为
是首项为![]() ,公比为3的等比数列,
,公比为3的等比数列,
故![]() ,
,
 ,
,
![]() ;
;
(3)![]()
即![]() 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列,
故![]() ,
,
记![]() ,
,
由(1)知
![]() ,
,![]()
证明:![]()
又![]()
![]() ,
,
即![]() ,
,
故![]()
![]()
两式相加得
![]()
![]()
![]() ,
,
即![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
【题目】![]() 年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分
年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分![]() 分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 不低于90分 |
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有![]() 人.
人.
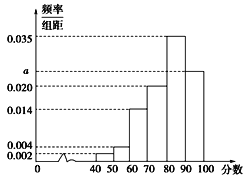
(1)求频率分布于直方图中![]() 的值,及评分等级不满意的人数;
的值,及评分等级不满意的人数;
(2)相关部门对项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.