题目内容
【题目】平面直角坐标系xoy中，直线l的参数方程是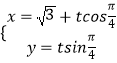 
（t为参数），以射线ox为极轴建立极坐标系，曲线C的极坐标方程是 
+ρ2sin2θ=1．
（1）求曲线C的直角坐标方程；
（2）求直线l与曲线C相交所得的弦AB的长．
【答案】
（1）
解：曲线C的极坐标方程是 
+ρ2sin2θ=1，把x=ρcosθ，y=ρsinθ代入可得： 
=1
（2）
解：直线l的参数方程是 
（t为参数），即 
，代入椭圆方程可得： 
﹣2=0，
∴t1+t2= 
，t1t2=﹣ 
，∴|AB|=|t1﹣t2|= 
= 
= 
【解析】（1）曲线C的极坐标方程是 +ρ2sin2θ=1，把x=ρcosθ，y=ρsinθ代入可得直角坐标方程．．（2）直线l的参数方程是 （t为参数），即 ，代入椭圆方程可得： ﹣2=0，利用|AB|=|t1﹣t2|= 即可得出
练习册系列答案
阅读快车系列答案
相关题目
