题目内容
14.已知等差数列{an}中a2=9,a5=21.(1)求数列{an}的通项公式;
(2)若${b_n}={2^{{a_n}-1}}$,求数列{log2bn}的前n项和Sn.
分析 (1)利用a5-a2=3d计算可得公差,进而可得结论;
(2)通过对数的性质化简可知数列$\left\{{log_2^{b_n}}\right\}$是以4为首项、4为公差的等差数列,进而计算可得结论.
解答 解:(1)∵a2=9,a5=21,
∴a5-a2=3d,∴d=4,
∴an=a2+(n-2)•d=4n+1;
(2)∵an=4n+1,
∴${b_n}={2^{{a_n}-1}}={2^{4n}}$,
∴log2$_2^{b_n}$=$log_2^{{2^{4n}}}$=4n,
∴数列$\left\{{log_2^{b_n}}\right\}$是以4为首项、4为公差的等差数列,
∴${S_n}=\frac{n(4+4n)}{2}=2{n^2}+2n$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,涉及对数的性质等基础知识,注意解题方法的积累,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
8.函数f(x)=2x+x3的零点所在区间为( )
| A. | (0,1) | B. | (-1,0) | C. | (1,2) | D. | (-2,-l) |
6.已知命题p:?x∈R,2x2+1>0,则¬p是( )
| A. | ?x∈R,2x2+1≤0 | B. | ?x0∈R,2x02+1>0 | C. | ?x0∈R,2x02+1<0 | D. | ?x0∈R,2x02+1≤0 |
2.某中学高一年级举办了一次科普知识竞赛,该竞赛分为预赛和决赛两个阶段.预赛为笔试,决赛为面试,现将所有参赛选手参加笔试的成绩(得分均为正数,满分100分)进行统计,制成如下频率分布表.
(Ⅰ)求出上表中的x,y,z,s,p的值;
(Ⅱ)按规定,预赛成绩不低于90分的选手将参加决赛,若高一②班有甲、乙两名同学取得决赛资格,现从中选出2人担任组长,求至少有一人来自高一②班的概率.
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合计 | p | 1 |
(Ⅱ)按规定,预赛成绩不低于90分的选手将参加决赛,若高一②班有甲、乙两名同学取得决赛资格,现从中选出2人担任组长,求至少有一人来自高一②班的概率.
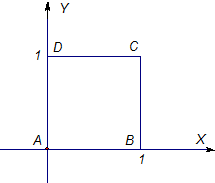 如图,在直角坐标系中,正方形ABCD的四个顶点分别为A(0,0),B(1,0),C(1,1),D(0,1).
如图,在直角坐标系中,正方形ABCD的四个顶点分别为A(0,0),B(1,0),C(1,1),D(0,1).


 是定义在实数集
是定义在实数集 上的奇函数,且当
上的奇函数,且当 时,
时, 成立,若
成立,若 ,则
,则 大小关系( )
大小关系( ) B.
B.
 D.
D.