题目内容
已知函数![]() 的图象是自原点出发的一条折线.当
的图象是自原点出发的一条折线.当![]() 时,该图象是斜率为
时,该图象是斜率为![]() 的线段(其中正常数
的线段(其中正常数![]() ),设数列
),设数列![]() 由
由![]() 定义. 求:
定义. 求:
求![]() 和
和![]() 的表达式;
的表达式;
求![]() 的表达式,并写出其定义域;
的表达式,并写出其定义域;
证明:![]() 的图像与
的图像与![]() 的图象没有横坐标大于1的交点.
的图象没有横坐标大于1的交点.
【小题1】依题意![]() ,又由
,又由![]() ,当
,当![]() 时,函数
时,函数![]() 的图象是斜率为
的图象是斜率为![]() 的线段,故由
的线段,故由![]() 得
得![]()
又由![]() ,当
,当![]() 时,函数
时,函数![]() 的图象是斜率为
的图象是斜率为![]() 的线段,故由
的线段,故由
![]() ,即
,即![]() 得
得![]()
记![]() 由函数
由函数![]() 的图象中第
的图象中第![]() 段线段的斜率为
段线段的斜率为![]() ,故得
,故得
![]()
又![]()
∴![]()
由此知数列![]() 为等比数列,其首项为1,公比为
为等比数列,其首项为1,公比为![]()
因![]() ,得
,得![]()

即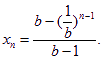
【小题2】当![]() 时,从(1)可知
时,从(1)可知![]() ,即当
,即当![]() 时,
时,![]()
当![]() 时,即当
时,即当![]() 时,由(1)可知
时,由(1)可知
![]()
为求函数![]() 的定义域,须对
的定义域,须对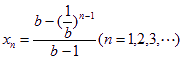 进行讨论.
进行讨论.
当![]() 时,
时,
![]() 时,
时,![]() ,
,![]() 也趋向于无穷大.
也趋向于无穷大.
综上,当![]() 时,
时,![]() 的定义域为
的定义域为![]()
当![]() 时,
时,![]() 的定义域为
的定义域为![]()
【小题3】证法1 首先证明当![]() 时,恒有
时,恒有![]() 成立.
成立.
对任意的![]() ,存在
,存在![]() 使
使![]() ,此时有
,此时有
![]()
![]()
又![]()
![]()
![]()
即有![]() 成立.
成立.
其次,当![]() ,仿上述证明,可知当
,仿上述证明,可知当![]() 时,恒有
时,恒有![]() 成立.
成立.
故函数![]() 的图象与
的图象与![]() 的图象没有横会标大于1的交点.
的图象没有横会标大于1的交点.
解析:
本题主要考查函数的基本概念、等比数列、数列极限的基础知识,考查归纳、推理和综合的能力.
【小题1】由斜率分式求出![]() ,同样由斜率公式求出关于
,同样由斜率公式求出关于![]() 的递推式,然后求出
的递推式,然后求出![]() ,
,
【小题2】由点斜式求出![]() 段的
段的![]() 的表达式,用极限的方法求出定义域.
的表达式,用极限的方法求出定义域.
【小题3】![]() 与
与![]() 没有交点,只要
没有交点,只要![]() 时
时![]() ,或
,或![]() 时
时![]() 恒成立,当
恒成立,当![]() ,由于
,由于![]() ,只要证
,只要证![]()

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 的图象是曲线C,点
的图象是曲线C,点 是曲线C上的一系列点,
是曲线C上的一系列点, 处的切线与y轴交于点
处的切线与y轴交于点 。若数列
。若数列 是公差为2的等差
是公差为2的等差
 与数列
与数列 表示
表示 的面积,求数列
的面积,求数列 的前项n和
的前项n和
 的图象经过原点,
的图象经过原点, 若
若 在
在 取得极大值2。
取得极大值2。 的解析式;
的解析式;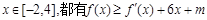 ,求
,求 的最大值。
的最大值。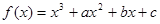 的图象过原点,且
的图象过原点,且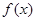 在
在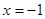 、
、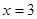 处取得极值.
处取得极值. 与
与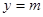 的图象有且仅有一个公共点,求实数
的图象有且仅有一个公共点,求实数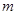 的取值范围.
的取值范围.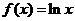 的图象是曲线C,点
的图象是曲线C,点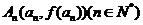 是曲线C上的一系列点,曲线C在点
是曲线C上的一系列点,曲线C在点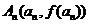 处的切线与y轴交于点
处的切线与y轴交于点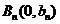 。若数列
。若数列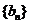 是公差为2的等差数列,且
是公差为2的等差数列,且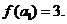
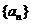 与数列
与数列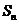 表示
表示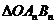 的面积,求数列
的面积,求数列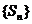 的前项n和
的前项n和