题目内容
已知函数 的图象是曲线C,点
的图象是曲线C,点 是曲线C上的一系列点,曲线C在点
是曲线C上的一系列点,曲线C在点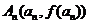 处的切线与y轴交于点
处的切线与y轴交于点 。若数列
。若数列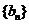 是公差为2的等差数列,且
是公差为2的等差数列,且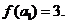
(1)分别求出数列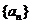 与数列
与数列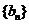 的通项公式;
的通项公式;
(2)设O为坐标原点, 表示
表示 的面积,求数列
的面积,求数列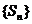 的前项n和
的前项n和
【答案】
解:在区间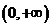 上,
上, .
……………………2分
.
……………………2分
①若 ,则
,则 ,
,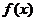 是区间
是区间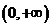 上的增函数,无极值; ………4分
上的增函数,无极值; ………4分
②若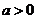 ,令
,令 得:
得:  .
.
在区间 上,
上,  ,函数
,函数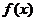 是增函数;
是增函数;
在区间 上,
上, 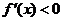 ,函数
,函数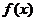 是减函数;
是减函数;
在区间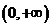 上,
上, 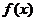 的极大值为
的极大值为 .
.
综上所述,①当 时,
时,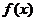 的递增区间
的递增区间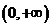 ,无极值; ………………7分
,无极值; ………………7分
③当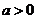 时,
时,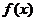 的是递增区间
的是递增区间 ,递减区间是
,递减区间是 ,
,
函数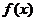 的极大值为
的极大值为 . ……………………9分
. ……………………9分
(2)  ∴
∴ ,解得:
,解得: .
……………………10分
.
……………………10分
∴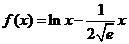 .
……………………11分
.
……………………11分
又 ,
, ,
, …………13分
…………13分
由(1)函数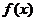 在
在 递减,故函数
递减,故函数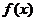 在区间
在区间 有唯一零点,
有唯一零点,
因此 .
……………………14分
.
……………………14分

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
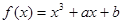 的图象是曲线C,直线
的图象是曲线C,直线 与曲线
与曲线 的解析式;
的解析式; 上的最大值和最小值.
上的最大值和最小值.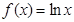 的图象是曲线C,点
的图象是曲线C,点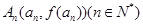 是曲线C上的一系列点,
是曲线C上的一系列点,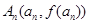 处的切线与y轴交于点
处的切线与y轴交于点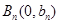 。若数列
。若数列 是公差为2的等差
是公差为2的等差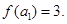
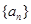 与数列
与数列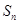 表示
表示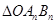 的面积,求数列
的面积,求数列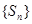 的前项n和
的前项n和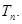
 的图象是一条连续的曲线,满足
的图象是一条连续的曲线,满足 ,下列说法正确的是( )
,下列说法正确的是( )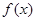 在
在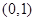 上至少有一个零点; B.
上至少有一个零点; B.