题目内容
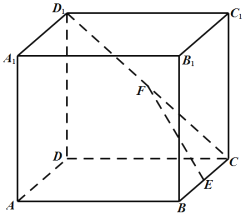
【题目】如图,在正方体![]() 中,
中, ![]() 分别是线段
分别是线段![]() 的中点.
的中点.
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:方法一:以![]() 为原点,直线
为原点,直线![]() ,
, ![]() ,
, ![]() 为
为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,求出直线
轴,建立空间直角坐标系,求出直线![]() 与
与![]() 的方向向量,可求两异面直线所成角,需要注意异面直线所成角范围是
的方向向量,可求两异面直线所成角,需要注意异面直线所成角范围是![]() 。线面角只需求出直线
。线面角只需求出直线![]() 的方向向量与平面
的方向向量与平面![]() 的法向量,利用公式可求解,注意线面角范围
的法向量,利用公式可求解,注意线面角范围![]() 。方法二:异面直线所成角另一种方法就是通过平移,把两异面直平移到同一平面。作
。方法二:异面直线所成角另一种方法就是通过平移,把两异面直平移到同一平面。作![]() 于
于![]() ,联结
,联结![]() ,有
,有![]() ∥
∥![]() ,故异面直线
,故异面直线![]() 与
与![]() 所成的角就是
所成的角就是![]() (或其补角).平面
(或其补角).平面![]() ∥平面
∥平面![]() ,故直线
,故直线![]() 与平面
与平面![]() 所成角的大小就是直线
所成角的大小就是直线![]() 与平面
与平面![]() 所成角.注意到
所成角.注意到![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,所以直线
,所以直线![]() 与平面
与平面![]() 所成角的大小即为
所成角的大小即为![]() .
.
试题解析:(1)方法一:设正方体棱长为![]() ,以
,以![]() 为原点,直线
为原点,直线![]() ,
, ![]() ,
, ![]() 为
为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,故
,故![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() ,向量
,向量![]() 与
与![]() 所成角为
所成角为![]() ,则
,则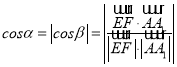
![]() ,注意到
,注意到![]() ,故
,故![]() ,即异面直线
,即异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
(2)由(1)可知,平面![]() 的一个法向量是
的一个法向量是![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角的大小是
所成角的大小是![]() ,向量
,向量![]() 与
与![]() 所成角为
所成角为![]() ,则
,则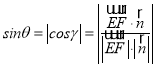
![]()
又![]() ,
, ![]() ,即直线
,即直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]()
方法二:设正方体棱长为![]() .
.
(1)在面![]() 内,作
内,作![]() 于
于![]() ,联结
,联结![]() .因为正方体
.因为正方体
![]() ,所以
,所以![]() ∥
∥![]() ;在面
;在面![]() 内,有
内,有![]() ∥
∥![]() ,故异面直线
,故异面直线![]() 与
与![]() 所成的角就是
所成的角就是![]() (或其补角).
(或其补角).
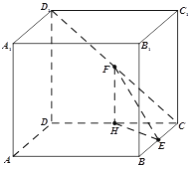
由已知及作图可知, ![]() 为
为![]() 的中点,于是,在
的中点,于是,在![]() 中,易得
中,易得![]() ,
,
![]() ,故
,故![]() ,
, ![]() ,
,
又![]() ,所以
,所以![]() ,从而异面直线
,从而异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
(2)因为正方体![]() ,所以平面
,所以平面![]() ∥平面
∥平面![]() ,故直线
,故直线![]() 与平面
与平面![]() 所成角的大小就是直线
所成角的大小就是直线![]() 与平面
与平面![]() 所成角.注意到
所成角.注意到![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,所以直线
,所以直线![]() 与平面
与平面![]() 所成角的大小即为
所成角的大小即为![]() .
.
在![]() 中,易得
中,易得![]() ,故
,故![]()
![]() ,
,
又![]() ,故
,故![]() ,即直线
,即直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.
点睛:对于长方体中求线线角,线面角的问题,规则图形用空间向量更容易解决。线线角的普通方法常用平移到同一个平面。线面角也是通过平移形成直线与平面相交,再在三角形中计算。

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】春节期间,“厉行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
做不到“光盘” | 能做到“光盘” | |
男 | 45 | 10 |
女 | 30 | 15 |
P(K2≥k) | 0.10 | 0.05 | 0.025 |
k | 2.706 | 3.841 | 5.024 |
附: ![]()
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别有关”
B.在犯错误的概率不超过l%的前提下,认为“该市居民能否做到‘光盘’与性别无关”
C.有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”
D.有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”