题目内容
设数列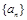 的前
的前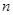 项和为
项和为 ,且满足
,且满足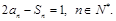
(1)求数列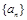 的通项公式;
的通项公式;
(2)在数列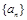 的每两项之间都按照如下规则插入一些数后,构成新数列
的每两项之间都按照如下规则插入一些数后,构成新数列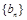 ,在
,在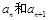 两项之间插入
两项之间插入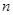 个数,使这
个数,使这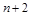 个数构成等差数列,求
个数构成等差数列,求 的值;
的值;
(3)对于(2)中的数列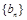 ,若
,若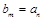 ,并求
,并求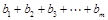 (用
(用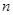 表示).
表示).
(1)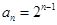 ;(2)
;(2)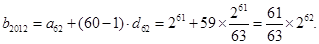
(3)
解析试题分析:(1)当 时,由
时,由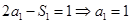 .又
.又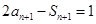 与
与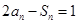 相减得:
相减得: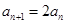 ,故数列
,故数列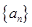 是首项为1,公 比为2的等比数列,所以
是首项为1,公 比为2的等比数列,所以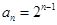 ; 4分
; 4分
(2)设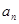 和
和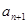 两项之间插入
两项之间插入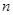 个数后,这
个数后,这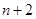 个数构成的等差数列的公差为
个数构成的等差数列的公差为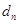 ,则
,则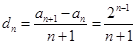 ,又
,又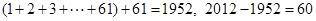 ,故
,故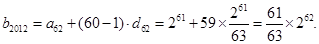 8分
8分
(3)依题意,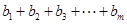
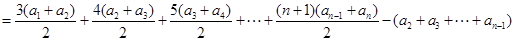
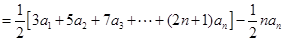 ,考虑到
,考虑到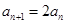 ,
,
令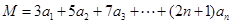 ,则
,则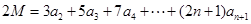
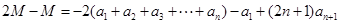
 ,
,
所以 12分
12分
考点:本题主要考查等差数列、等比数列的概念及其通项公式,数列的求和。
点评:典型题,本题首先由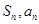 的关系,确定数列的通项公式是关键。求和过程中应用了“错位相减法”。在数列问题中,“分组求和法”“裂项相消法”也常常考到。
的关系,确定数列的通项公式是关键。求和过程中应用了“错位相减法”。在数列问题中,“分组求和法”“裂项相消法”也常常考到。

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
已知数列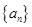 ,
,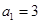 ,
,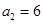 ,且
,且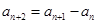 ,则数列的第五项为( )
,则数列的第五项为( )
A. | B.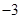 | C.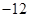 | D.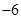 |
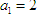 ,点
,点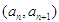 在函数
在函数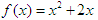 的图象上,其中
的图象上,其中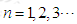
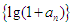 是等比数列,并求数列
是等比数列,并求数列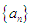 的通项公式;
的通项公式; ,求数列
,求数列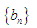 的前
的前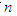 项和
项和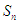 .
.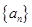 的首项
的首项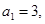 前
前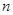 项和为
项和为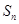 ,且
,且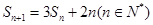 ,
,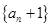 是否成等比数列?并求出数列
是否成等比数列?并求出数列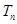 为数列
为数列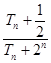 的最小值.
的最小值.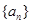 的前
的前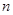 项和为
项和为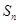 ,且
,且 ,
,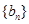 满足
满足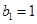 ,且点
,且点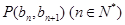 在直线
在直线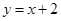 上.
上.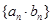 的前
的前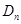 ;
;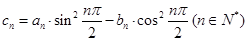 ,求数列
,求数列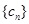 的前
的前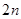 项和
项和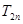 .
.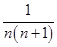 .
. 的前
的前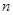 项和为
项和为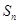 ,且
,且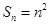 .数列
.数列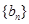 为等比数列,且
为等比数列,且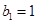 ,
,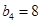 .
. 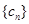 满足
满足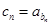 ,求数列
,求数列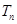 .
.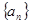 的通项公式为
的通项公式为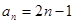 ,数列
,数列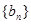 的前n项和为
的前n项和为 ,且满足
,且满足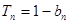
 中是否存在使得
中是否存在使得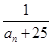 是
是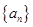 的前n项和为
的前n项和为 ,且满足
,且满足 ,n=1,2,3,…….
,n=1,2,3,……. 满足
满足 ,且
,且 ,求数列
,求数列 ,求数列
,求数列 的前n项和
的前n项和 .
.