题目内容
设数列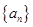 的前n项和为
的前n项和为 ,且满足
,且满足 ,n=1,2,3,…….
,n=1,2,3,…….
(1)求数列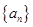 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,且
,且 ,求数列
,求数列 的通项公式;
的通项公式;
(3)设 ,求数列
,求数列 的前n项和
的前n项和 .
.
(1) 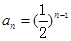 (2)
(2) 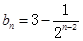
解析试题分析:解:(1)当n=1时,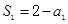 ,所以
,所以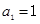
当n≥2时, 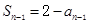 ,且
,且
所以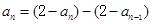 得:
得: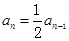
则数列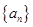 是以1为首项,
是以1为首项,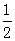 为公比的等比数列,
为公比的等比数列,
所以:数列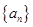 的通项公式是
的通项公式是 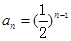 。
。
(2) 由  且
且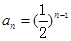 所以:
所以: ,
,
则: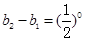 ,
,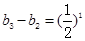 ,
,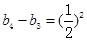 ?? ?
?? ?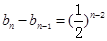 ,
,
以上n-1个等式叠加得: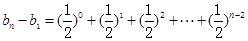
则: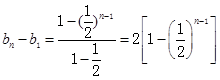 =2-
=2-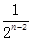 ,又
,又
所以: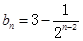
考点:数列的通项公式的求解
点评:利用通项公式与前n项和的关系式来求解得到,属于基础题。

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
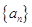 的前n项和为
的前n项和为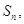 已知
已知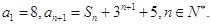
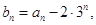 证明:数列
证明:数列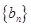 是等比数列;
是等比数列;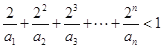 .
.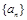 的前
的前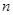 项和为
项和为 ,且满足
,且满足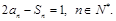
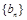 ,在
,在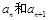 两项之间插入
两项之间插入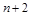 个数构成等差数列,求
个数构成等差数列,求 的值;
的值;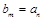 ,并求
,并求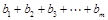 (用
(用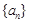 的前
的前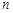 项和为
项和为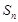 ,且
,且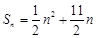 。数列
。数列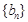 满足
满足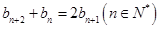 ,
,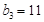 ,
,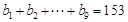 。
。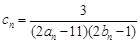 ,数列
,数列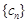 的前
的前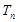 ,求使不等式
,求使不等式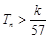 对一切
对一切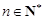 都成立的最大正整数
都成立的最大正整数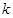 的值;
的值;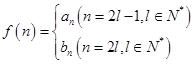 ,是否存在
,是否存在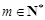 ,使得
,使得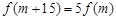 成立?若存在,求出
成立?若存在,求出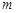 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。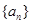 中,
中, 为其前
为其前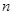 项和,满足
项和,满足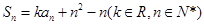 .
.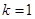 ,求数列
,求数列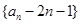 为公比不为1的等比数列,求
为公比不为1的等比数列,求 ,
,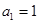 ,前
,前 项和为
项和为 .各项均为正数的等比数列列
.各项均为正数的等比数列列 满足:
满足: ,
, ,且
,且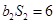 .
.
 的首项为2,点
的首项为2,点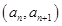 在函数
在函数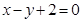 的图像上
的图像上 项之和为
项之和为 ,求
,求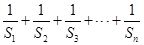 的值.
的值. 的前
的前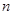 项和
项和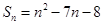 ,
,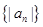 的前
的前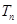 .
.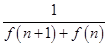 ,n∈N*.记数列{an}的前n项和为Sn,则S2013=( )
,n∈N*.记数列{an}的前n项和为Sn,则S2013=( )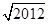 -1
-1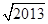 -1
-1 -1
-1