题目内容
在平面四边形ABCD中,△ABC为正三角形,△ADC为等腰直角三角形,AD=DC=2,将△ABC沿AC折起,使点B至点P,且PD=2 ,M为PA的中点,N在线段PD上.
,M为PA的中点,N在线段PD上.

(I)若PA⊥平面CMN,求证:AD∥平面CMN;
(II)求直线PD与平面ACD所成角的余弦值.
(I)证明:∵AD=2,PA= ,PD=2
,PD=2
∴PA2+AD2=PD2,∴PA⊥AD
∵PA⊥平面CMN,∴PA⊥MN
∴MN∥AD
∵AD?平面CMN,MN?平面CMN,
∴AD∥平面CMN;
(II)解:取AC中点E,连接ED、PE,过P作PF⊥ED交ED于F
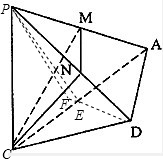
∵△APC为正三角形,∴AC⊥PE
∵AD=DC,∴AC⊥DE
∵PE∩DE=E,∴AC⊥平面PED
∵PF?平面PED
∴PF⊥AC,PF⊥BD,AC∩ED=E
∴PF⊥平面ACD
∴∠PDE为直线PD与平面ACD所成的角
在△PDE中,∵PE= ,ED=
,ED= ,PD=2
,PD=2
∴cos∠PDE=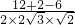 =
=
∴直线PD与平面ACD所成角的余弦值为 .
.
分析:(I)先证明PA⊥AD,利用PA⊥平面CMN,可得PA⊥MN,从而可得MN∥AD,利用线面平行的判定,可得AD∥平面CMN;
(II)取AC中点E,连接ED、PE,过P作PF⊥ED交ED于F,则可得∠PDE为直线PD与平面ACD所成的角,在△PDE中,利用余弦定理,可求直线PD与平面ACD所成角的余弦值.
点评:本题考查线面平行,考查线面角,掌握线面平行的判定,正确作出线面角是关键.
 ,PD=2
,PD=2
∴PA2+AD2=PD2,∴PA⊥AD
∵PA⊥平面CMN,∴PA⊥MN
∴MN∥AD
∵AD?平面CMN,MN?平面CMN,
∴AD∥平面CMN;
(II)解:取AC中点E,连接ED、PE,过P作PF⊥ED交ED于F

∵△APC为正三角形,∴AC⊥PE
∵AD=DC,∴AC⊥DE
∵PE∩DE=E,∴AC⊥平面PED
∵PF?平面PED
∴PF⊥AC,PF⊥BD,AC∩ED=E
∴PF⊥平面ACD
∴∠PDE为直线PD与平面ACD所成的角
在△PDE中,∵PE=
 ,ED=
,ED= ,PD=2
,PD=2
∴cos∠PDE=
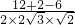 =
=
∴直线PD与平面ACD所成角的余弦值为
 .
.分析:(I)先证明PA⊥AD,利用PA⊥平面CMN,可得PA⊥MN,从而可得MN∥AD,利用线面平行的判定,可得AD∥平面CMN;
(II)取AC中点E,连接ED、PE,过P作PF⊥ED交ED于F,则可得∠PDE为直线PD与平面ACD所成的角,在△PDE中,利用余弦定理,可求直线PD与平面ACD所成角的余弦值.
点评:本题考查线面平行,考查线面角,掌握线面平行的判定,正确作出线面角是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
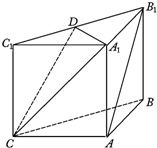 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.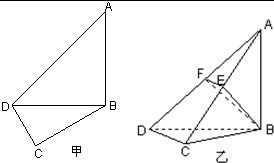 在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.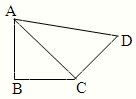 如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.
如图,在平面四边形ABCD中,AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿对角线AC将此四边形折成直二面角.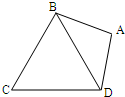 (2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,
(2007•武汉模拟)如图,在平面四边形ABCD中,AB=AD=1,∠BAD=θ,而△BCD是正三角形,