题目内容
曲线 上的动点
上的动点 是坐标为
是坐标为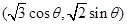 .
.
(1)求曲线 的普通方程,并指出曲线的类型及焦点坐标;
的普通方程,并指出曲线的类型及焦点坐标;
(2)过点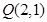 作曲线
作曲线 的两条切线
的两条切线 、
、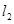 ,证明
,证明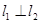 .
.
(1) ,焦点在
,焦点在 轴的椭圆 ,焦点坐标为
轴的椭圆 ,焦点坐标为 ;(2)证明见解析.
;(2)证明见解析.
解析试题分析:(1)由动点坐标得 ,消去参数可得
,消去参数可得 的普通方程,由方程可知曲线为椭圆,且求出焦点坐标;(2)易知过Q的直线斜率不存在时与曲线C无交点,不相切,设过Q的直线
的普通方程,由方程可知曲线为椭圆,且求出焦点坐标;(2)易知过Q的直线斜率不存在时与曲线C无交点,不相切,设过Q的直线 ,与椭圆方程联立得
,与椭圆方程联立得 ,由切知
,由切知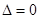 ,即
,即 ,又斜率积为
,又斜率积为 ,则
,则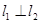 .
.
试题解析:
解:(1) -2分
-2分
焦点在 轴的椭圆 , -4分
轴的椭圆 , -4分
焦点坐标为 . -6分
. -6分
(2)易知过Q的直线斜率不存在时与曲线C无交点,不相切; -7分
设过Q的直线 ,
,
由 得
得 ,
,
若 与曲线C相切则
与曲线C相切则 ,
,
得 ,则
,则 ,
,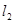 的斜率为方程的两根,
的斜率为方程的两根,
有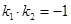 , -11分
, -11分 . -12分
. -12分
考点:参数方程,直线垂直时斜率间的关系.

练习册系列答案
相关题目
 ,
,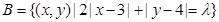 ,若
,若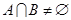 ,则实数
,则实数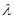 的取值范围是__________.
的取值范围是__________. ,点
,点 在直线
在直线 上运动,当线段
上运动,当线段 最短时,点
最短时,点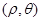
 中,曲线
中,曲线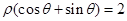 与
与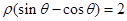 的交点的极坐标为________
的交点的极坐标为________
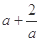 恒成立,则实数a的取值范围______
恒成立,则实数a的取值范围______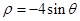 和
和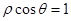 相交于点
相交于点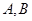 ,则线段
,则线段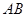 的长度为 .
的长度为 . .
. 过原点,且被曲线C截得弦长最短,求此时直线
过原点,且被曲线C截得弦长最短,求此时直线 是曲线C上的动点,求
是曲线C上的动点,求 的最大值.
的最大值.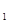 :
: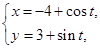 (t为参数), C
(t为参数), C :
: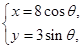 (
(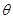 为参数)。
为参数)。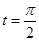 ,Q为C
,Q为C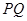 中点
中点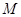 到直线
到直线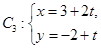 (t为参数)距离的最小值。
(t为参数)距离的最小值。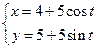 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为 .
. 中,曲线
中,曲线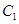 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,得曲线
轴的非负半轴为极轴建立极坐标系,得曲线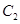 的极坐标方程为
的极坐标方程为 (
( )
)  :
:  (
( 为参数)过曲线
为参数)过曲线 轴负半轴的交点,求与直线
轴负半轴的交点,求与直线