题目内容
 是函数
是函数 在区间
在区间 上为减函数的
上为减函数的
| A.充分非必要条件 | B.必要非充分条件 | C.充要条件 | D.非充分非必要条件 |
A
解析试题分析:对于 ,当
,当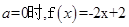 满足在区间
满足在区间 上为减函数;当
上为减函数;当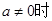 ,要满足题意需
,要满足题意需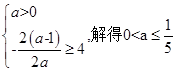 。综上知满足函数
。综上知满足函数 在区间
在区间 上为减函数的a的范围是
上为减函数的a的范围是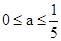 。所以
。所以 是函数
是函数 在区间
在区间 上为减函数的充分非必要条件。
上为减函数的充分非必要条件。
考点:函数的单调性;二次函数的性质。
点评:此题是易错题,错误的原因忽略了对二次项系数的讨论。一般情况下,若二次项系数含有字母,要对二次项系数是否为0进行讨论。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
给出命题:已知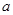 、
、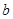 为实数,若
为实数,若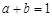 ,则
,则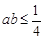 .在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( ).
.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( ).
| A.3 | B.2 | C.1 | D.0 |
“ ”是“曲线
”是“曲线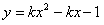 恒在
恒在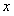 轴下方”的( )条件
轴下方”的( )条件
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既非充分又非必要 |
“ ”是“直线
”是“直线 和
和 平行”的( )
平行”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列有关命题的说法正确的是 ( )
A.命题“若 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若 ,则 ,则 ”. ”. |
B.“ ”是“ ”是“ ”的必要不充分条件. ”的必要不充分条件. |
C.命题“ 使得 使得 ”的否定是:“ ”的否定是:“ 均有 均有 ”. ”. |
D.命题“若 ,则 ,则 ”的逆否命题为真命题. ”的逆否命题为真命题. |
下列命题中,真命题是( )
A.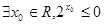 | B.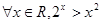 |
C.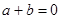 的充要条件是 的充要条件是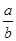 =-1 =-1 | D.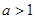 且 且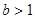 是 是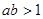 的充分条件 的充分条件 |
设 ,则“
,则“ 且
且 ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
某学习小组对函数 进行研究,得出了如下四个结论:①函数
进行研究,得出了如下四个结论:①函数 在
在 上单调递增;②存在常数
上单调递增;②存在常数 对一切实数
对一切实数 均成立;③函数
均成立;③函数 在
在 上无最小值,但一定有最大值;④点
上无最小值,但一定有最大值;④点 是函数
是函数 的一个对称中心,其中正确的是
的一个对称中心,其中正确的是
| A.①③ | B.②③ | C.②④ | D.①②④ |
已知命题p: ,则
,则 为( )。
为( )。
A. , , | B.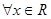 , , |
C. , , | D.: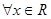 , , |