题目内容
(本小题满分16分)
在任何两边都不相等的锐角三角形ABC中,已知角A、B、C的对边分别为a、b、c
且
(1)求角B的取值范围;
(2)求函数 的值域; (3)求证:
的值域; (3)求证:
在任何两边都不相等的锐角三角形ABC中,已知角A、B、C的对边分别为a、b、c
且

(1)求角B的取值范围;
(2)求函数
 的值域; (3)求证:
的值域; (3)求证:
(1) (2)(
(2)( );(3)
);(3)
 (2)(
(2)( );(3)
);(3)
第一问利用∵
∴
∴ ∴
∴
第二问 …………5分
…………5分
由(Ⅰ)得 ∴
∴ ,∴函数
,∴函数 的值域为(
的值域为(
解:(1)∵
∴ …………2分
…………2分
∴ ∴
∴ …5分
…5分
(若本小题未去除60度,则扣1分)
(2)∵ …………5分
…………5分
由(Ⅰ)得 …………6分
…………6分
∴ ,∴函数
,∴函数 的值域为(
的值域为( ).……10分
).……10分
(若本小题值域含端点2,则扣1分)
(3)∵ ∴
∴
 ,∵
,∵
∴ ∴
∴ …………16分
…………16分

∴

∴
 ∴
∴
第二问
 …………5分
…………5分由(Ⅰ)得
 ∴
∴ ,∴函数
,∴函数 的值域为(
的值域为(
解:(1)∵

∴
 …………2分
…………2分∴
 ∴
∴ …5分
…5分(若本小题未去除60度,则扣1分)
(2)∵
 …………5分
…………5分由(Ⅰ)得
 …………6分
…………6分∴
 ,∴函数
,∴函数 的值域为(
的值域为( ).……10分
).……10分(若本小题值域含端点2,则扣1分)
(3)∵
 ∴
∴
 ,∵
,∵
∴
 ∴
∴ …………16分
…………16分
练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
 ,cos(α-β)=
,cos(α-β)= ,且0<β<α<
,且0<β<α<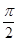 .
. ,
, .求值:①
.求值:① ;②
;② .
.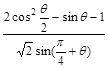 的值. (2)求
的值. (2)求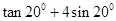 的值.
的值.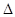 ABC中,
ABC中,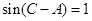 , sinB=
, sinB=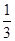 .
.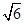 ,求
,求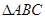 中,
中,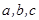 分别是角A、B、C的对边,
分别是角A、B、C的对边,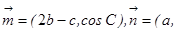
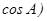 ,且
,且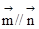 .
.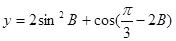 的值域.
的值域. ,则
,则 的值为
的值为



 ,那么
,那么 = .
= .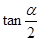 =2,则
=2,则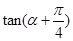 的值为
的值为