题目内容
(12分)在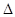 ABC中,
ABC中,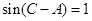 , sinB=
, sinB=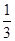 .
.
(I)求sinA的值;
(II)设AC=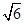 ,求
,求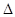 ABC的面积.
ABC的面积.
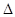 ABC中,
ABC中,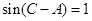 , sinB=
, sinB=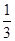 .
.(I)求sinA的值;
(II)设AC=
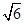 ,求
,求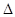 ABC的面积.
ABC的面积.(Ⅰ)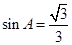
(Ⅱ)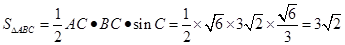
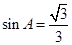
(Ⅱ)
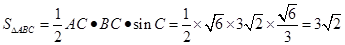
(1) 由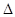 ABC中,
ABC中,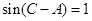 ,得
,得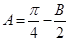
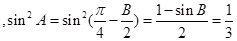 。
。
∴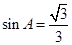
(2)由(1)和正弦定理得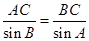 ,
,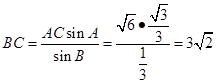 ,
,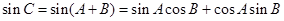
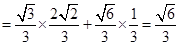 。
。
所以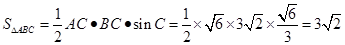 。
。
解:(Ⅰ)由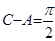 ,且
,且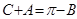 ,∴
,∴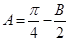 ,∴
,∴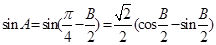 ,
,
∴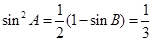 ,又
,又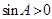 ,∴
,∴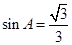
(Ⅱ)如图,
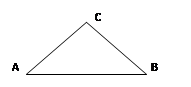
由正弦定理得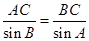
∴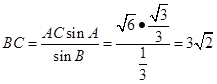 ,又
,又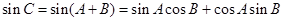
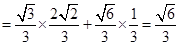
∴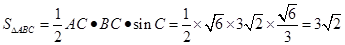
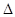 ABC中,
ABC中,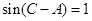 ,得
,得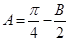
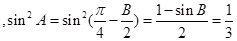 。
。∴
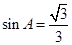
(2)由(1)和正弦定理得
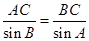 ,
,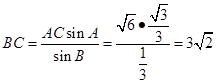 ,
,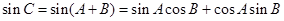
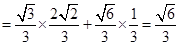 。
。所以
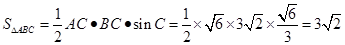 。
。解:(Ⅰ)由
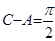 ,且
,且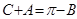 ,∴
,∴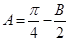 ,∴
,∴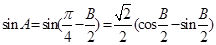 ,
,∴
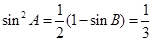 ,又
,又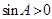 ,∴
,∴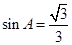
(Ⅱ)如图,
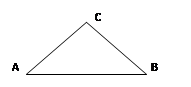
由正弦定理得
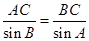
∴
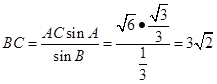 ,又
,又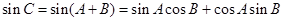
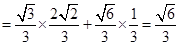
∴
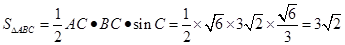

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 ,cos(α+β)=
,cos(α+β)=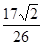 ,且α∈(π,
,且α∈(π,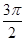 ),α+β∈(
),α+β∈( ,求
,求 的值.
的值.
 的值域; (3)求证:
的值域; (3)求证:
 ,求下列各式的值:
,求下列各式的值:


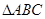 中,角
中,角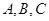 所对边的长分别为
所对边的长分别为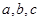 ,且
,且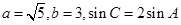 .
.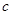 的值;(2)求
的值;(2)求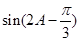 的值.
的值.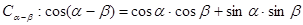 ;
;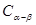 推导两角和的余弦公式
推导两角和的余弦公式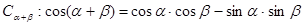 .
.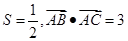 ,且
,且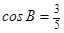 ,求
,求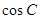 .
.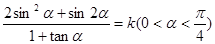 ,则
,则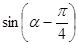 的值 ( )
的值 ( ) 的增大而减小
的增大而减小  ,
, ,则
,则 =
=