题目内容
已知cosα= ,cos(α-β)=
,cos(α-β)= ,且0<β<α<
,且0<β<α<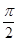 .
.
(1)求tan2α的值;
(2)求β的值.
 ,cos(α-β)=
,cos(α-β)= ,且0<β<α<
,且0<β<α<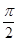 .
.(1)求tan2α的值;
(2)求β的值.
(1) -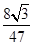 (2)
(2) 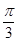
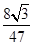 (2)
(2) 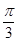
本试题主要是考查了两角和差的三角函数变换的运用,以及构造角的思想求解角的 综合运用。
(1)由cosα= ,0<α<
,0<α<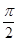 ,
,
得sinα=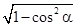 =
=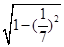 =
=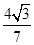 ,
,
∴tanα=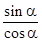 =
=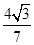 ×
×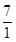 =
=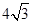 .
.
从而结合二倍角公式得到结论。
(2)由β=α-(α-β)
cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)=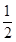
那么利用由0<β<α<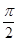 ,得0<α-β<
,得0<α-β<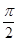 .
.
又∵cos(α-β)= ,得到各个三角函数值,求解得到结论。
,得到各个三角函数值,求解得到结论。
(1)由cosα= ,0<α<
,0<α<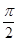 ,
,
得sinα=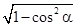 =
=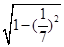 =
=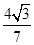 ,
,
∴tanα=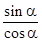 =
=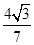 ×
×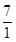 =
=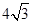 .
.
于是tan2α=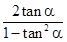 =
=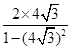
=-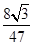 . ………6分
. ………6分
(2)由0<β<α<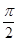 ,得0<α-β<
,得0<α-β<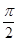 .
.
又∵cos(α-β)= ,
,
∴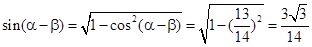
由β=α-(α-β)
cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)=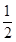
又∵0<β<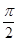
∴β=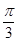 ……13分
……13分
(1)由cosα=
 ,0<α<
,0<α<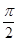 ,
,得sinα=
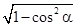 =
=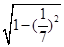 =
=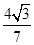 ,
,∴tanα=
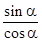 =
=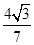 ×
×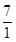 =
=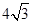 .
.从而结合二倍角公式得到结论。
(2)由β=α-(α-β)
cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)=
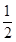
那么利用由0<β<α<
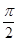 ,得0<α-β<
,得0<α-β<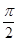 .
.又∵cos(α-β)=
 ,得到各个三角函数值,求解得到结论。
,得到各个三角函数值,求解得到结论。(1)由cosα=
 ,0<α<
,0<α<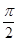 ,
,得sinα=
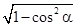 =
=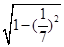 =
=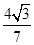 ,
,∴tanα=
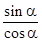 =
=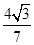 ×
×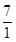 =
=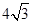 .
.于是tan2α=
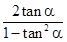 =
=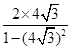
=-
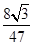 . ………6分
. ………6分(2)由0<β<α<
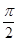 ,得0<α-β<
,得0<α-β<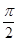 .
.又∵cos(α-β)=
 ,
,∴
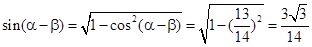
由β=α-(α-β)
cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)=
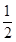
又∵0<β<
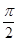
∴β=
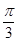 ……13分
……13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
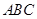 中,角
中,角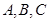 的对边分别为
的对边分别为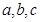 ,已知
,已知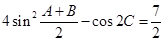 ,且
,且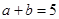 ,
,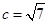 ,求: (Ⅰ)
,求: (Ⅰ)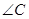 .⑾△
.⑾△ ,
, ,
, ,
, ,求
,求 的值.
的值. ,cos(α+β)=
,cos(α+β)=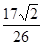 ,且α∈(π,
,且α∈(π,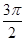 ),α+β∈(
),α+β∈( ,
, ).
). |=|
|=| |,求角α的值;
|,求角α的值;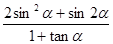 的值.
的值.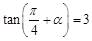 ,且
,且 为锐角.
为锐角. 的值;
的值; 的值.
的值.
 的值域; (3)求证:
的值域; (3)求证:
 中,若
中,若 ,则
,则 和
和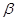 都是锐角,且
都是锐角,且 ,
, ,则
,则 的值是( )
的值是( )  B.
B. C.
C. D
D