题目内容
【题目】如图,![]() 是正方形空地,边长为
是正方形空地,边长为![]() ,电源在点P处,点P到边
,电源在点P处,点P到边![]() 距离分别为
距离分别为![]() .某广告公司计划在此空地上竖一块长方形液晶广告屏幕
.某广告公司计划在此空地上竖一块长方形液晶广告屏幕![]() ,
,![]() ,线段
,线段![]() 必须过点P,端点
必须过点P,端点![]() 在边
在边![]() 上,端点
上,端点![]() 在正方形
在正方形![]() 的边上,设
的边上,设![]() ,液晶广告屏幕
,液晶广告屏幕![]() 的面积为
的面积为![]() .
.
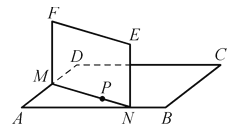
(1)用![]() 的代数式表示AM;
的代数式表示AM;
(2) 求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)当![]() 取何值时,液晶广告屏幕
取何值时,液晶广告屏幕![]() 的面积
的面积![]() 最小?
最小?
【答案】(1) ![]() ;(2)
;(2)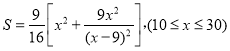 (3)
(3)![]() .
.
【解析】
(1)由![]() 对应边成比例即可表示AM;
对应边成比例即可表示AM;
(2)由(1)得到的结论,根据勾股定理用![]() 表示MN,再由
表示MN,再由![]() ,可以用
,可以用![]() 表示NE,即能表示面积S,结合
表示NE,即能表示面积S,结合![]() 为边长求定义域即可;
为边长求定义域即可;
(3)根据(2),求出函数的导函数,利用函数的导数求函数在给定区间上的最小值即可.
解:(1) 过点P作AB的垂线,垂足于G
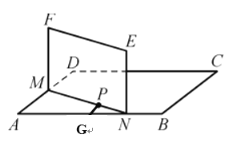
由题意可知:![]()
所以![]()
![]() ;
;
(2)![]() .
.
![]()
![]()
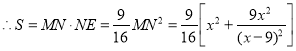 .
.
定义域为![]() .
.
(3)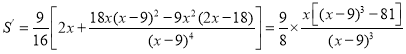 ,
,
令![]() ,得
,得![]() (舍),
(舍),![]() .(13分)
.(13分)
当![]() 时,
时,![]() ,S关于
,S关于![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,S关于
,S关于![]() 为增函数;
为增函数;
![]() 当
当![]() 时,S取得最小值.
时,S取得最小值.
答:当AN长为![]() 时,液晶广告屏幕MNEF的面积S最小.
时,液晶广告屏幕MNEF的面积S最小.

【题目】某仪器经过检验合格才能出厂,初检合格率为![]() :若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为
:若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为![]() .每台仪器各项费用如表:
.每台仪器各项费用如表:
项目 | 生产成本 | 检验费/次 | 调试费 | 出厂价 |
金额(元) | 1000 | 100 | 200 | 3000 |
(Ⅰ)求每台仪器能出厂的概率;
(Ⅱ)求生产一台仪器所获得的利润为1600元的概率(注:利润![]() 出厂价
出厂价![]() 生产成本
生产成本![]() 检验费
检验费![]() 调试费);
调试费);
(Ⅲ)假设每台仪器是否合格相互独立,记![]() 为生产两台仪器所获得的利润,求
为生产两台仪器所获得的利润,求![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
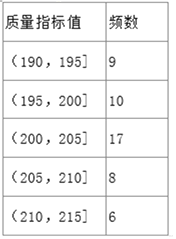
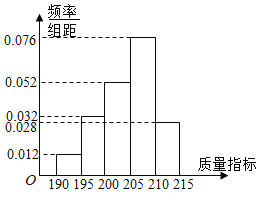
(1)根据频率分布直方图,估计乙流水线生产的产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲流水线 | 乙流水线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |