题目内容
设方程2x2+x+p=0的解集为A,方程2x2+qx+2=0的解集为B,A∩B={
},求A∪B.
| 1 | 2 |
分析:根据两集合的交集中的元素属于A又属于B,将x的值代入方程求出p与q的值,即可确定出两集合的并集.
解答: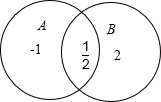 解:∵A∩B={
解:∵A∩B={
},∴
∈A,
∈B,
将x=
代入2x2+x+p=0得:
+
+p=0,即p=-1;将x=
代入2x2+qx+2=0得:
+
q+2=0,即q=-5,
又方程2x2+x-1=0的解为x=-1或x=
;方程2x2-5x+2=0的解为x=
或2,
∴A={-1,
},B={
,2},
则A∪B={-1,
,2}.
 解:∵A∩B={
解:∵A∩B={| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
将x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又方程2x2+x-1=0的解为x=-1或x=
| 1 |
| 2 |
| 1 |
| 2 |
∴A={-1,
| 1 |
| 2 |
| 1 |
| 2 |
则A∪B={-1,
| 1 |
| 2 |
点评:此题考查了并集及其运算,以及交集及其运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.