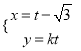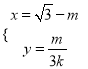题目内容
【题目】求适合下列条件的双曲线的标准方程：
(1)过点(3，－
)，离心率e＝
；
(2)中心在原点，焦点F1，F2在坐标轴上，实轴长和虚轴长相等，且过点P(4，－
)．
【答案】（1）
； （2）
.
【解析】
（1）根据题意，由双曲线的离心率
，得到a=2b，然后分焦点在x轴和焦点在y轴设出标准方程，将点(3，－
)代入计算即可得双曲线的方程．（2）由实轴长和虚轴长相等得a=b,即双曲线为等轴双曲线，设出等轴双曲线方程，将点坐标代入即可得答案.
(1)若双曲线的焦点在x轴上，设其标准方程为
(a＞0，b＞0)．
因为双曲线过点(3，－)，则
.①
又e＝
，故a2＝4b2.②
由①②得a2＝1，b2＝
，故所求双曲线的标准方程为
.
若双曲线的焦点在y轴上，设其标准方程为
(a＞0，b＞0)．
同理可得b2＝－
，不符合题意．
综上可知，所求双曲线的标准方程为.
(2)由2a＝2b得a＝b，所以 e＝
，
所以可设双曲线方程为x2－y2＝λ(λ≠0)．
因为双曲线过点P(4，－
)，
所以 16－10＝λ，即λ＝6.
所以 双曲线方程为x2－y2＝6.
所以 双曲线的标准方程为
.
练习册系列答案
相关题目
【题目】去年年底，某商业集团公司根据相关评分细则，对其所属25家商业连锁店进行了考核评估.将各连锁店的评估分数按[60,70), [70,80), [80,90), [90,100),分成四组，其频率分布直方图如下图所示，集团公司依据评估得分，将这些连锁店划分为A,B,C,D四个等级，等级评定标准如下表所示.
评估得分 | [60,70) | [70,80) | [80,90) | [90,100) |
评定等级 | D | C | B | A |
（1）估计该商业集团各连锁店评估得分的众数和平均数；
（2）从评估分数不小于80分的连锁店中任选2家介绍营销经验，求至少选一家A等级的概率.
