题目内容
(09年青岛质检理)(12分)
在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 为矩形,
为矩形,![]() .
.
(Ⅰ)当![]() 时,求证:
时,求证:![]() ;
;
(Ⅱ) 若![]() 边上有且只有一个点
边上有且只有一个点![]() ,使得
,使得![]() ,求此时二面角
,求此时二面角![]() 的余弦值.
的余弦值.
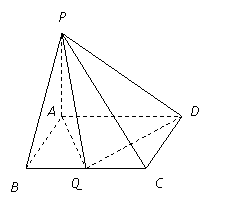
解析:(Ⅰ)当![]() 时,底面
时,底面![]() 为正方形,
为正方形,![]()
![]()
又因为![]() ,
,![]() 面
面![]() …………………………2分
…………………………2分
又![]() 面
面![]()
![]() …………………………3分
…………………………3分
(Ⅱ) 因为![]() 两两垂直,分别以它们所在直线
两两垂直,分别以它们所在直线
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立坐标系,如图所示,
轴建立坐标系,如图所示,
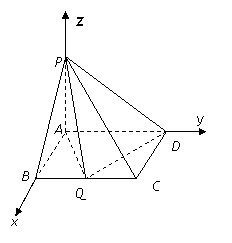
则![]() …………………4分
…………………4分
设![]() ,则
,则![]()
要使![]() ,只要
,只要![]()
所以![]() ,即
,即![]() ………6分
………6分
由此可知![]() 时,存在点
时,存在点![]() 使得
使得![]()
当且仅当![]() ,即
,即![]() 时,
时,
![]() 边上有且只有一个点
边上有且只有一个点![]() ,使得
,使得![]()
由此可知![]() …………………………8分
…………………………8分
设面![]() 的法向量
的法向量![]()
则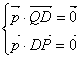 即
即![]() 解得
解得![]() …………………………10分
…………………………10分
取平面![]() 的法向量
的法向量![]()
则![]() 的大小与二面角
的大小与二面角![]() 的大小相等
的大小相等
所以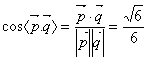
因此二面角![]() 的余弦值为
的余弦值为![]() …………………………12分
…………………………12分

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目