题目内容
已知椭圆C: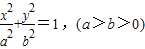 ,直线(m+3)x+(1-2m)y-m-3=0(m∈R)恒过的定点F为椭圆的一个焦点,且椭圆上的点到焦点F的最大距离为3,
,直线(m+3)x+(1-2m)y-m-3=0(m∈R)恒过的定点F为椭圆的一个焦点,且椭圆上的点到焦点F的最大距离为3,(1)求椭圆C的方程;
(2)若直线MN为垂直于x轴的动弦,且M、N均在椭圆C上,定点T(4,0),直线MF与直线NT交于点S.求证:
①点S恒在椭圆C上;
②求△MST面积的最大值.
【答案】分析:(1)化直线方程为直线系方程,然后联立方程组求出定点F的坐标,得到c的值,然后由椭圆上的点到焦点F的最大距离为3得到a+c=3,求出a的值,结合b2=a2-c2可得b得值,则答案可求;
(2)①设出直线MN的方程,求出M和N的坐标,然后写出MF和NF所在的直线方程,联立后得到S点的坐标,代入椭圆方程后成立,则问题得到证明.
②设出直线MS的方程,和椭圆方程联立后化为关于y的一元二次方程,利用根与系数关系得到M,S两点的纵坐标的和与积,然后代入面积公式,换元后利用“对勾函数”的单调性求得答案.
解答:解:(1)直线(m+3)x+(1-2m)y-m-3=0可化为
m(x-2y-1)+3x+y-3=0,
所以 ,解得
,解得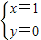 .
.
所以F(1,0).则c=1,又a+c=3,所以a=2,则b2=a2-c2=3.
所以椭圆方程为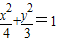 ;
;
(2)①设直线MN的方程为x=s,M的坐标为(s,t),N的坐标为(s,-t).
且s、t满足3s2+4t2=12.
MF的直线方程为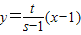 ,NT的直线方程为
,NT的直线方程为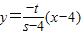 .
.
联立解得交点S(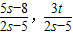 ),代入椭圆方程3x2+4y2=12得,
),代入椭圆方程3x2+4y2=12得,
3(5s-8)2+36t2=12(2s-5)2,化简得:3s2+4t2=12.
所以点S恒在椭圆C上;
②直线MS过点F(1,0),设方程为x=my+1,M(x1,y1),S(x2,y2).
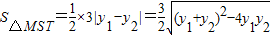 .
.
联立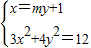 ,得(3m2+4)y2+6my-9=0.
,得(3m2+4)y2+6my-9=0.
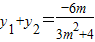 ,
,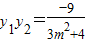 .
.
所以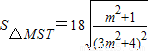 .
.
设m2+1=u(u≥1),则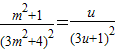 =
=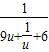 .
.
由对勾函数可知9u+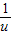 在(
在(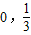 )上位减函数,(
)上位减函数,(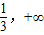 )上为增函数,
)上为增函数,
所以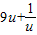 的最小值为10.
的最小值为10.
所以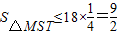 .
.
点评:本题考查了椭圆的简单几何性质,考查了直线和圆锥曲线的关系,训练了“设而不求”的解题方法,考查了利用函数的单调性求最值,该题综合性较强,需要学生具有较好的理解能力和计算能力,是难题.
(2)①设出直线MN的方程,求出M和N的坐标,然后写出MF和NF所在的直线方程,联立后得到S点的坐标,代入椭圆方程后成立,则问题得到证明.
②设出直线MS的方程,和椭圆方程联立后化为关于y的一元二次方程,利用根与系数关系得到M,S两点的纵坐标的和与积,然后代入面积公式,换元后利用“对勾函数”的单调性求得答案.
解答:解:(1)直线(m+3)x+(1-2m)y-m-3=0可化为
m(x-2y-1)+3x+y-3=0,
所以
 ,解得
,解得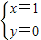 .
.所以F(1,0).则c=1,又a+c=3,所以a=2,则b2=a2-c2=3.
所以椭圆方程为
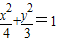 ;
;(2)①设直线MN的方程为x=s,M的坐标为(s,t),N的坐标为(s,-t).
且s、t满足3s2+4t2=12.
MF的直线方程为
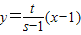 ,NT的直线方程为
,NT的直线方程为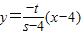 .
.联立解得交点S(
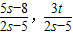 ),代入椭圆方程3x2+4y2=12得,
),代入椭圆方程3x2+4y2=12得,3(5s-8)2+36t2=12(2s-5)2,化简得:3s2+4t2=12.
所以点S恒在椭圆C上;
②直线MS过点F(1,0),设方程为x=my+1,M(x1,y1),S(x2,y2).
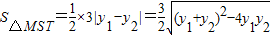 .
.联立
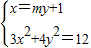 ,得(3m2+4)y2+6my-9=0.
,得(3m2+4)y2+6my-9=0.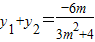 ,
,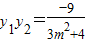 .
.所以
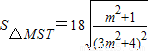 .
.设m2+1=u(u≥1),则
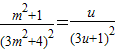 =
=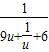 .
.由对勾函数可知9u+
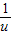 在(
在(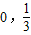 )上位减函数,(
)上位减函数,(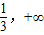 )上为增函数,
)上为增函数,所以
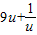 的最小值为10.
的最小值为10.所以
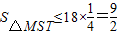 .
.点评:本题考查了椭圆的简单几何性质,考查了直线和圆锥曲线的关系,训练了“设而不求”的解题方法,考查了利用函数的单调性求最值,该题综合性较强,需要学生具有较好的理解能力和计算能力,是难题.

练习册系列答案
相关题目
 ,直线l:y=ax+b(a,b∈R)
,直线l:y=ax+b(a,b∈R)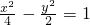 ,或改为抛物线方程y2=4x,再在第(4)问添加的条件中选择一个,求出直线l的方程.
,或改为抛物线方程y2=4x,再在第(4)问添加的条件中选择一个,求出直线l的方程.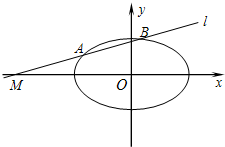 已知椭圆C:
已知椭圆C: ,直线l过点M(m,0).
,直线l过点M(m,0).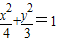 ,直线l过点M(m,0).
,直线l过点M(m,0).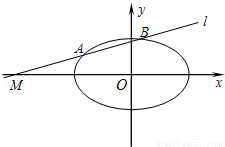
 ,直线l与椭圆C相交于A、B两点,
,直线l与椭圆C相交于A、B两点, (其中O为坐标原点).
(其中O为坐标原点).